| The polynomial coefficients divided by gaps |
| Integer value of degree |
|
|
| The received polynom as a result of exponentiation |
Let's develop our work on studying of polynomials. So, we are already able to multiply them and it turns out at us well. Now our task construction of any polynomial of a look
where b, c.... z, w - are polynom coefficients.
in integer degree.
Actually the objective turns into a task multiplication of an initial polynomial on itself so many time how many degree matters
If degree is equal to eleven, then it is necessary to multiply 11 times a polynomial on itself. And as it was already told in the first lines of article, we are able to multiply.
It would be desirable to notice that the polynomial may contain both the valid, and imaginary numbers that undoubtedly increases chances of this calculator to be noticed on Internet open spaces.
The number of coefficients of a polynomial is not limited, and here degree is limited from above to number 30, in avoidance of the raised load of the server. Let's review an example of exponentiation 3 polynomials
The answer which will give the boat
Other example, we will build in the 13th degree here such complex polynomial
The answer is following
As it is possible to notice the resulting polynomial it is symmetric concerning number 212941. Probably it is possible to connect these coefficients with the well-known triangle of Pascal somehow.
Successful calculations!
|
|



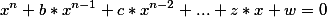
^3)
=x^{6}+(9)*x^{5}+(12)*x^{4}+(-63)*x^{3}+(-60)*x^{2}+(225)x+(-125))
^{13})
=(0+i)*x^{26}+(0-13i)*x^{25}+(0+91i)*x^{24}+(0-442i)*x^{23}+(0+1651i)*x^{22}+(0-5005i)*x^{21}+(0+12727i)*x^{20}+(0-27742i)*x^{19}+(0+52624i)*x^{18}+(0-87802i)*x^{17}+(0+129844i)*x^{16}+(0-171106i)*x^{15}+(0+201643i)*x^{14}+(0-212941i)*x^{13}+(0+201643i)*x^{12}+(0-171106i)*x^{11}+(0+129844i)*x^{10}+(0-87802i)*x^{9}+(0+52624i)*x^{8}+(0-27742i)*x^{7}+(0+12727i)*x^{6}+(0-5005i)*x^{5}+(0+1651i)*x^{4}+(0-442i)*x^{3}+(0+91i)*x^{2}+(0-13i)x+(0+i))