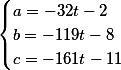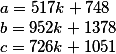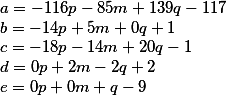The coefficients of the first diophantine equation
The coefficients of the second diophantine equation
The system of two diophantine equations General decision matrix String result Check for the first equation Check for the second equation
An original algorithm for solving two arbitrary homogeneous linear equations in integers is considered. Automatic calculation of decision matrix.
Let us need to solve a system of two Diophantine equations
$$\begin{alignedat}{3}2&a-11&b+13&c=1\\62&a+22&b-73&c=-31\end{alignedat}$$
Undoubtedly, you can solve this system as they do everything.
- Multiplying the first equation by 31 and subtracting from the second we get the classical Diophantine equation with two variables.
- Having decided which one can find all integer values of the system
The working scheme, despite a lot of manual calculations
I do not like this approach and we will use a different method for the solution.
It is beautiful and understandable even for students who know about vectors and matrices.
Partially used is the algorithm described here in this article (p. 36.37)
It is finalized, reduced to matrix operations and generalized to any values.
We will study the algorithm and its work using an example.
We solve the following system of diophantine equations
$$\begin{alignedat}{3}49&a+22&b-26&c=12\\70&a-31&b+9&c=9\end{alignedat}$$
We took this example for the reason that it was solved on the Internet and a general solution was developed for it. So there is something to compare.
1. We find the general solution of the first equation from a given system. For example, let it be
8 14 20 -19 -30 -44 -1 1 0
$$\begin{cases}a=8m+14p+20\\b=-19m-30p-44\\c=-m+p+0\end{cases}$$
How to verify that this is a true equality? Yes, just multiply the coefficient vector of the first equation by the resulting matrix
$$\begin{pmatrix}49&22&-26\\\end{pmatrix}*\begin{pmatrix}8&14&20\\-19&-30&-44\\-1&1&0\\\end{pmatrix}=\begin{pmatrix}0&0&12\\\end{pmatrix}$$
As you can see, the answer coincides with the free term of the first equation.
2. Now, since we have found a general solution to the first equation, let's substitute it into the second.
That is, in the equation $$70a-31b+9c=9$$ substitute our values
$$\begin{cases}a=8m+14p+20\\b=-19m-30p-44\\c=-m+p+0\end{cases}$$
You can substitute and reduce this with your hands, but in matrix calculus we only multiply the vector {70, -31,9} by our matrix.
$$\begin{pmatrix}70&-31&9\\\end{pmatrix}*\begin{pmatrix}8&14&20\\-19&-30&-44\\-1&1&0\\\end{pmatrix}=\begin{pmatrix}1140&1919&2764\\\end{pmatrix}$$
That is, we got the equation
\(1140m+1919p+2764=0\)
But, note that in the second equation the free term is not zero, but nine.
That is, we rewrite
We transfer the free terms to the right side and get the classical Diophantine equation, which we can solve easily.
The general solution is
3. Now do the inverse transformation.
I.e
into this system
instead of unknowns, we substitute the found m and p.
In matrix calculus, this is solved as follows:
We remove from the matrix 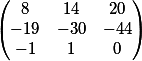
got
Multiply this matrix by the matrix created from these equations
we get
The last column is free members, add to it the column that was removed at the beginning of this paragraph
that is, to the vector {-22 36 -11} we add {20 -44 0}
We get the system
Therefore, the general solution of the system of two diophantine equations
takes on the form
Check if they counted correctly
For the first equation
For the second
As you can see, the values of the free terms coincide with the values on the right side of the equations, and therefore we got a general solution.
But it’s too early to rejoice, despite the fact that we got a general solution, we do not get all the possible values.
Why? Yes, because the vector \(\{-608 -2261 -3059\}\) has GCD = 19
and in fact our general solution is
Since the numbers in brackets must be integers, we denote them by t and ours, already exactly the final general solution to the system of two Diophantine equations, has the form
Some more examples, and small remarks to the algorithm.
answer
another example
answer
As you can see, it is possible to solve unlimited in the number of variables diophantine equations.
Now that calculator cannot.
Very much does not like equations with zero coefficients. Especially the first. For example, such a system
the calculator will not solve.
*x_{1}+(3)*x_{2}+(0)*x_{3}+(6)*x_{4}+(-5)*x_{5}=19\\) |
Well, how does he not decide? Decides if we resort to the trick, and try to remove all zero coefficients
Add to the first equation, the second. Thus, in the first equation, all zero coefficients disappear and the calculator can solve this system
| The system of two diophantine equations |
*x_{1}+(3)*x_{2}+(-7)*x_{3}+(12)*x_{4}+(-5)*x_{5}=17\\) |
*x_{1}+(3)*x_{2}+(0)*x_{3}+(6)*x_{4}+(-5)*x_{5}=19\\) |
| General decision matrix |
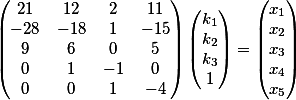 |
Verification shows that the general solution is correct.
And another example
| The system of two diophantine equations |
*x_{1}+(1)*x_{2}+(-7)*x_{3}+(6)*x_{4}+(1)*x_{5}+(-2)*x_{6}+(-13)*x_{7}+(11)*x_{8}+(7)*x_{9}+(2)*x_{10}+(3)*x_{11}=12\\) |
*x_{1}+(-1)*x_{2}+(6)*x_{3}+(-5)*x_{4}+(9)*x_{5}+(0)*x_{6}+(3)*x_{7}+(17)*x_{8}+(-13)*x_{9}+(-100)*x_{10}+(142)*x_{11}=-190\\) |
| General decision matrix |
 |
Good luck with your calculations !!



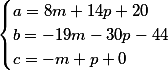
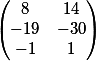
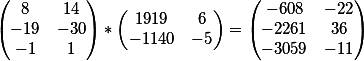
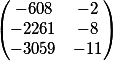
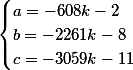
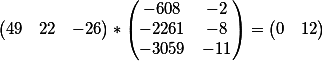
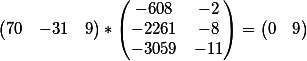
-2\\b=-119(19k)-8\\c=-161(19k)-11\end{cases})