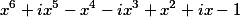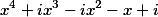| Initial polynom (its coefficients) |
| we divide into the following polynom / polynomial |
|
|
| Initial polynom |
| The dividing polynomial |
| Result of division |
| Remainder of division of two polynoms |
| General view |
The division of arbitrary polynomials (polynomials) into each other with separation of the remainder from division is considered. The method used in this article is fundamentally different from other calculators of this type, which use the "column" method. Undoubtedly, for students and pupils who have just begun to study this topic, the "column" method is much clearer and simpler.
But for calculations where increased accuracy and speed of calculations are needed, the generalized Horner method is used , the main difference of which is that the division function is not used in the calculation process, which introduces errors in the final calculation.
The calculator I created also works great in the field of complex numbers, which will undoubtedly increase the efficiency of its use.
The generalized method of division we will consider a little later in the same material, and now, a few examples.
Split polynomial 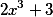
input coefficients will be like this
and the result of the division
Another example of division of complex polynomials. I wanted to find examples on the Internet, but apparently no one ever covered this topic: neither examples, nor solutions.
Well then...
"Who is the extreme king here? Nobody? So I will be the first" (c)
Divide a polynomial of the form
in polynomial
Enter in the first field 1 i -1 -i 1 i -1 (These are the coefficients of the first polynomial)
In the second field 1 i -i -1 i (These are the coefficients of the second polynomial)
And we get the answer
| Source polynomial |
*x^{5}+(-1)*x^{4}+(-i)*x^{3}+(1)*x^{2}+(i)*x+(-1)) |
| Dividing polynomial |
*x^{3}+(-i)*x^{2}+(-1)*x+(i)) |
| Division result |
) |
| The remainder of the division of two polynomials |
*x^{3}+(0-2i)*x^{2}+(-1+2i)*x+(0+1i)) |
| General form |
*x^{5}+(-1)*x^{4}+(-i)*x^{3}+(1)*x^{2}+(i)*x+(-1)%20=%20\\(x^{2}+(-1+1i))*(x^{4}+(i)*x^{3}+(-i)*x^{2}+(-1)*x+(i))\\%20+%20(2)*x^{3}+(0-2i)*x^{2}+(-1+2i)*x+(0+1i)) |
In the future here, or as a separate article, I will write what patterns can be found when dividing polynomials.
And also since we can divide polynomials, then we can find its GCD
GCD of two polynomials. Greatest Common Factor (GCF)
Good luck!




}=2+\frac{(-2)*x+3}{(x^{3}+x)})