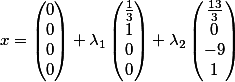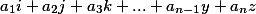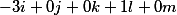Each equation or is transferred to a new line or divided by a semicolon
Initial system of the equations Fundamental System of Decisions (FSD) of this system of the equations Base system/denominator
Let's try to solve a system of equations, such as
The solution of such systems is inextricably linked with the formula for reducing the matrix to a triangular form. It is clear, beautiful and never fails. There is only one thing but, you need to do a lot of manual work and use the concepts of matrix rank
There is no doubt about exposing technology that has been proven over the centuries, but there is an equally beautiful solution using a vector product . There is no information on them on January 2019 on the Internet, so we modestly call ourselves the discoverer.
This solution, of course, is not optimal (in terms of speed), since when calculating a vector product, it is necessary to calculate the determinant of the matrix, and this is somehow the calculation of the triangular matrix.
But the solution is beautiful and clear, besides this it is easy to see the criterion under which the system has no solutions.
What is the essence of the technique?
Solving this system as the product of two vectors, we obtain
Consequently, the roots of the system are equal
For those who do not believe, this is easily verified by substitution.
The same simple technique is used in systems where the number of variables can be five and ten.
Let us consider how such systems are solved using vector products.
So we have the source system
We bring it in this form
We got 6 columns.
At this stage, we will not introduce new entities and will not use the concepts of matrix rank in our work. We just see that there are 3 equations, and 5 variables. Therefore, the general solution will use 5-3 = 2 independent variables.
At the same step, we can determine which of the variables will be free. Since fantasies are zero, then those of the variables that will be to the right of all, those will become free.
That is, we will have two variables free
And now in three steps we determine the fundamental solution of the original system
Step 1.
Step 2
Step 3
There is no need to tell in detail where we get the data from. It is obvious
What is more interesting is what we will do with these "vectors".
Divide them by -81
we get the following three vectors
Thus, the fundamental decision takes the form
Sumptuously! Is not it....
I would like to solve something .... Another example
This is an interesting equation, since vectors in any combination will give zero.
This tells us that one of the equations is "superfluous." We agree with this and remove it. For example, the latter.
Then we need to choose two free variables, let it be variables with indices 2 and 4.
Then the vectors are found as
Divide by -3 and our general solution will look like
It is not immediately clear to everyone where we get zeros and ones in our slender vector series. This is due to the fact that we chose free variables as our heart desires, and not the most extreme right ones.
If we took the variables with indices 3 and 4 as free then we would rewrite the solution as the machine would give us.
At the beginning of the article, we mentioned the criterion of the unsolvability of a particular system of equations. In the classical version, the Kronecker-Copelli rule is used for this, here the result of the vector product is simply analyzed.
If the resulting vector has the form
Where 
Examples of unsolvable systems of equations
If the resulting vector has all zero coefficients (we considered such an example above), then this suggests that either at least one of the equations is a linear representation of the other, and / or one of the variables is proportional to the other.
The calculator presented here gives you the opportunity to analyze the source system yourself, it will only make accurate calculations for you according to the data that you enter to it.
Here is one example
| The original system of equations |
*x_{1}+(2)*x_{2}+(3)*x_{3}+(4)*x_{4}+(5)*x_{5}+(6)*x_{6}+(7)=0\\(5)*x_{1}+(6)*x_{2}+(7)*x_{3}+(8)*x_{4}+(9)*x_{5}+(10)*x_{6}+(11)=0\\(-3)*x_{1}+(1)*x_{3}+(4)*x_{6}+(8)=0\\) |
| The fundamental system of solutions (SDF) of this system of equations |
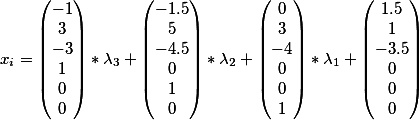 |
| System Base / Denominator |
 |



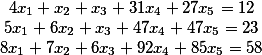
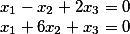
i%20+%20(%201%20)j%20+%20(%207%20)k)
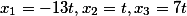
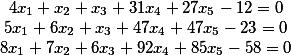
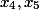
i%20+%20(%20-162%20)j%20+%20(%20-486%20)k%20+%20(%20-81%20)l)
i%20+%20(%20162%20)j%20+%20(%20405%20)k%20+%20(%20-81%20)l)
i%20+%20(%20243%20)j%20+%20(%20324%20)k%20+%20(%20-81%20)l)

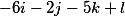
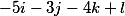
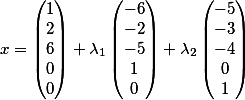
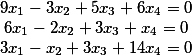
i%20+%20(%20-0%20)j%20+%20(%200%20)k%20+%20(%200%20)l)
i%20+%20(%20-0%20)j%20+%20(%20-0%20)k%20+%20(%200%20)l)
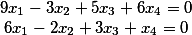
i%20+%20(%20-0%20)j%20+%20(%20-3%20)k)
i%20+%20(%20-0%20)j%20+%20(%20-3%20)k)
i%20+%20(%2027%20)j%20+%20(%20-3%20)k)