| Matrix elements |
|
|
| Matrix form of record of this square form |
The calculation of the quadratic form is a fairly simple task, at least the descriptive part is primitive to impossibility and the calculation algorithm, when the matrix is known, consists in calculating each of the elements according to the formula
Where, 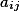
But everything is primitive, does not mean convenient, and it is easy to make mistakes when calculating a quadratic form. Our calculator will help you not to make mistakes in the calculations.
As with all calculators, a matrix can contain not only real numbers, but also complex ones.
When entering data, we have two fields:
the first is the matrix;
the second is a way to name each element.
If in the second field we write some sort of character (a, b, c ....) then each element will be named
Let's look at a few examples.
Enter the elements of the matrix with a space (you can start each row with a new line)
and get the following results
Complex field calculation
Good calculations !!



=\sum%20_{{i,j=1}}^{n}a_{{ij}}x_{i}x_{j})
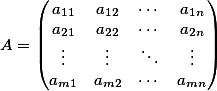
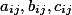
x_{0}^2}+(2)x_{0}x_{1}+(4)x_{0}x_{2}+(3)x_{1}^2}+(1)x_{2}^2})
a_{0}^2}+(4)a_{0}a_{1}+(-2)a_{0}a_{2}+(-5)a_{1}^2}+(6)a_{1}a_{2}+(8)a_{2}^2})
s_{0}^2+(4-1i)s_{0}s_{1}+(-7+1i)s_{0}s_{2}+(-1)s_{0}s_{3}+(2)s_{1}^2+(2.4-2i)s_{1}s_{2}+(7+1i)s_{1}s_{3}+(11)s_{2}^2+(-6-1i)s_{2}s_{3}+(2i)s_{3}^2)