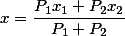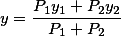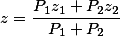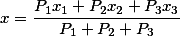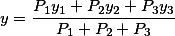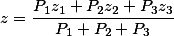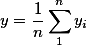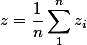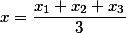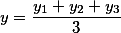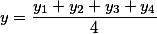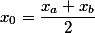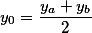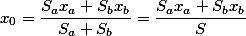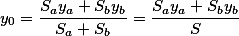| The polygon coordinates divided by gaps. Can have a+ib appearance | |
| Alternative partitioning (if the current one is incorrect) | |
| YES | |
|
| |
| You entered the following coordinates of a polygon |
| Coordinates of the center of gravity |
| The area of the set polygon (in conventional units) |
To create crafts, puzzles, and simply in household chores, sometimes a situation arises when it is necessary to calculate the center of gravity of a figure. And if for the simplest figures, the formulas for calculating the center of gravity are known, for example, for a circle the center of gravity coincides with the center of the circle, then more complex figures, and even more so figures consisting of broken lines, are very difficult to calculate manually.
What is a center of gravity? This is such a point on the figure, raising beyond which, the figure remains in the same position as it lay, for example, on the table. This is an amateurish explanation of course, besides this we are talking about flat figures. A more correct one is: The center of gravity of a mechanical system is the point relative to which the total moment of gravity acting on the system is zero .
The calculator calculates the center of gravity of any flat, uniform composition, consisting of broken lines.
What do you, as a user, need to know? The coordinates of the points of the vertices of such a polygon are required.
How to determine the center of gravity?
If parallel forces act on points M1 (x1, y1, z1) and M2 (x2, y2, z2 ), then the point M of application of the resultant of these forces divides the segment M1M2 inversely to these forces
Therefore, the coordinates of point M will be
if we are talking about the effect of three acting forces, then the formulas are similar and are calculated as the arithmetic weighted average
in the same way they are calculated if, at the points of application of forces, not three, but four or five or ten, for example.
If we assume that the force acting on the points will be gravity, and the mass of the points will be the same, then after the reductions of the same values, our formula for the three points will be as follows
Here the position of the center of gravity depends only on the position of the points. Point () is called the geometric center of gravity of these points.
If the figure is symmetrical, then the center of gravity coincides with the geometric center of the figure. This applies for example to figures such as a square, a circle, a regular polygon, an equilateral triangle, and other similar objects.
And yet, a little theory that will help calculate the center of gravity of complex figures.
The position of the center of gravity of the system of point masses does not change if any partial group of point masses of the system is replaced by one point mass located in the center of gravity of this group and having as the mass the sum of the masses of points of this group.
CALCULATION OF THE CENTER OF GRAVITY OF THE TRIANGLE ON COORDINATES
We calculate the center of gravity of a triangular plate, of arbitrary shape, of the same thickness.
What material we are going to make from steel, paper or a platik is not so important.
The center of gravity of a triangle is one of seven remarkable points, and is defined as the point of intersection of the medians of the sides of this triangle.
If we know only the coordinates of the triangle, for example, we cut it from a notebook into a cell, then the coordinates of the point of gravity will be determined as follows
Do not try to approximate this formula and think that the center of the trapezoid will be calculated similarly, for example, by such formulas
This is not true, or rather, incorrect in the case when the mass is distributed in a plane between these points (for example, a plate).
If we are talking about point masses located in these coordinates, then the formula of the center of mass will be correct.
CALCULATION OF THE GRAVITY CENTER OF THE TRAPEZE BY COORDINATES
How then to calculate the center of gravity of the trapezoid?
Smart people found the formula for calculating the point, but in it the source data is presented as the lengths of the sides of the trapezoid.
Here is the formula.
It is not convenient when we know only the coordinates of the trapezoid. But we will use the method of splitting the trapezoid two triangles, where for each of them we find the center of gravity, and then calculating for two points (centers), we find the final solution.
For each triangle, the center will be calculated using the well-known formula
But now, when we will calculate the final point, we must take into account that we, "pulling together" each triangle into the center of gravity, we also pull together the entire mass of the surface that lay between these coordinates.
Since there is a linear relationship between the area of the figure (with the same thickness) and mass, it is easy to assume that the final calculation will be different
and taking into account the linearity between the mass and the area (which means you can not calculate the mass of each new point, but only take into account the area of each of the two triangles), the formula for the trapezoid will be
Moreover, this formula will be workable for any arbitrary polygon, the only condition is that the areas of each of the triangle do not intersect with each other.
So, we have a figure with coordinates 0: 0 5: 5 10: 5 15: 0
It is easy to imagine this figure and determine that it is an equilateral trapezoid.