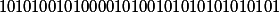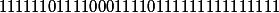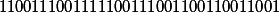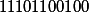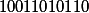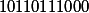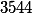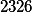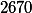| Integer number |
| Numeral system |
|
|
| The original value of the binary |
| From the source to the gray code(binary) |
| From gray's code to the original (binary) |
| The original value in the specified calculus |
| From the source to the gray code(set calculus) |
| From gray's code to the original (given calculus) |
The calculator allows you to convert a given number into gray's code, and do automatic reverse conversion.
The property of these codes is that when a number is changed to an adjacent one, the binary bits composing it changed only in one position.
Dec Bin Gray
0 0000 0000
1 0001 0001
2 0010 0011
3 0011 0010
4 0100 0110
5 0101 0111
6 0110 0101
7 0111 0100
8 1000 1100
9 1001 1101
10 1010 1111
11 1011 1110
12 1100 1010
13 1101 1011
14 1110 1001
15 1111 1000
As you can see, the neighboring numbers represented by the gray code change only one, and only one bit.
Where can this be applied? For example, in biology, when the genome chain can be encoded by the gray code, and then the minimum mutation in one position, will mean a change in one position of the gray code, and therefore the number in the decimal system will differ only by one.
Gray's code can be created only for binary representations of numbers, in other number systems, codes like gray's code can not be created.
But! No one forbids us to take any integer in any number system, translate it into binary form, apply gray's code and return it back to the original number system.
Our calculator does that. It produces the result in both the original number system and binary. In my opinion it is very convenient.
For example, taking our decimal system and then the number 343 in gray's code looks like 508. With one click, the number 343 was converted to binary, gray's code was extracted from it, and the number was converted to decimal again.
How to convert hexadecimal number gray code and back again, better than Wikipedia is not written. Algorithms are also taken from there.
Some examples of transformations
Input
1010100101000010100101010101010101
Answer:
| The original value of the binary |
 |
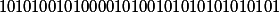| From the source to the gray code(binary) |
 |
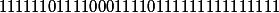| From gray's code to the original (binary) |
 |
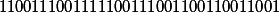| The original value in the specified calculus |
|
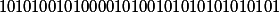| From the source to the gray code(set calculus) |
|
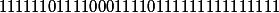| From gray's code to the original (given calculus) |
|
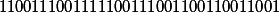Example2:
| Integer number |
| Numeral system |
| 8 |
| The original value of the binary |
 |
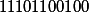| From the source to the gray code(binary) |
 |
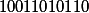| From gray's code to the original (binary) |
 |
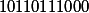| The original value in the specified calculus |
 |
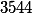| From the source to the gray code(set calculus) |
 |
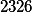| From gray's code to the original (given calculus) |
 |