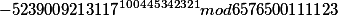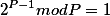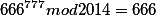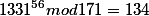| The basis the degree and the module divided at least by one gap |
|
|
| The received result |
Let's consider one of tasks often meeting in arithmetics and the theory of numbers which can be expressed several examples.
What rest the following numbers will have
if to try to divide them into number 31?
And if the first example can be solved on the calculator, so to speak "in a forehead, without thinking", then as you will solve the third example, it for some very not a trivial task.
What is the rest? The rest in this case is such number (on absolute value less module!), which having taken away from initial number, the received result will be is divided totally into the module (in our example the module this number 31)
That is, if we designate the rest a letter X we will receive (in the first example) that the number 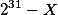
Or in another, record more habitual
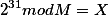
How to solve similar problems?
For this purpose we should know several properties from the theory of numbers which we will show on the second example
1.
Even to explain a reluctance, we put-1 outside "brackets" (a separate multiplier) and we can count at once. If degree of number (321) even the result is equal 1 if odd-1.
2.
If number it is possible to present that in the form of two and more factors, the rest from this number will be equal to the work of the remains from factors on the same module.
3.
Having added or having taken away the whole number of the module from any factor - the rest will not change.
4.
Too nothing difficult, just transformed degree. Usual property of degrees.
5.
Here we cubed-5 and used the 3rd rule, having added to it 4 times the module
6.
Having used the first rule, received that our answer 1
That is we can claim that 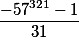
7.The last rule says that is formal, there are always two rests and they are equivalent. In our example it is 1 and-30 as 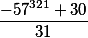
I hope it a small example of analysis, gave you a technique of the solution of similar tasks.
And the boat which is created will help you to learn easily correctness of the solution of similar tasks or if you the teacher, easily and precisely to generate tasks for pupils.
Each element may contain up to 19 figures (in general I do not know on what length, there can be mistakes, but at (to) 19 symbols everything works well)
therefore there is nothing terrible to find the rest here from such "monster"
who wants can multiply on the calculator:)
answer 3848922529426
INTERESTING FACTS
It is claimed that if P - that a prime number is carried out here such equality
This condition necessary (that is it is applicable to all prime numbers) but not sufficient (that is there are composite numbers for which this formula is valid too)
Beautiful expression was found so far tested the boat (for 2014):)
For May 31, 2018 still there was something interesting
You look



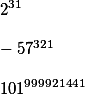
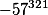
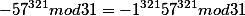
57^{321}mod31=(-1)mod31*57^{321}mod31)
^{321}mod31=-1*(-5)^{321}mod31)
^{321}mod31=-1*(-5^3)^{\frac{321}{3}}mod31=-1*(-5^3)^{107}mod31)
^{107}mod31=-1*(-125)^{107}=-1*(-125+31+31+31+31)^{107}mod31)
^{107}mod31=-1*(-1)^{107}mod31=-1*-1mod31=1)