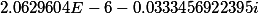| Polynom coefficients 4 degrees |
|
|
| Initial polynomial |
| Cubic rezolventa |
| Roots of a cubic rezolventa |
| Roots of the set polynomial 4 degrees |
| Auxiliary coefficients |
| F2= |
| F1= |
| T= |
This calculator allows to calculate roots of any polynom of the fourth degree.
Coefficients can be both real and complex numbers.
A certain technique which is not described anywhere and is not sorted was used.
Did not begin to use formulas Ferrari - not interestingly.
Despite an own way, you utykatsya all the same in a task of the solution of the auxiliary equation of the third degree, a so-called cubic rezolventa. And most likely to avoid it it will not turn out in any way.
But further everything goes on another.
On any of value of a root of a rezolventa, we calculate three auxiliary parameter.
Knowing these three parameters, we can easily find all four roots of the initial equation.
There is only one nuance which predecessors faced, I should sometimes some define a sign + or too - for one auxiliary parameter.
Now in the form of formulas
Replacement substitution 
We look for the solution of this equation in the form of the sums of two functions
Three auxiliary parameters are connected to coefficients of the given polynom through the following ratios
Expressing any of auxiliary parameters we receive, in this or that look a cubic rezolventa
For example if we express F2
This cubic equation, which substitution 
Now about which spoke about nuance earlier. What sign to take when we calculate roots?
The criterion turns out very simple. We take any root of a rezolventa and we compare it
if this condition true is put + (plus), if a condition incorrect - (minus)
Further all these parameters are substituted in a formula
+F(T,F_2))
Still it would be desirable to talk about criterion. The thoughtful reader will ask: "And what if any root of a rezolventa is complex number? What in this case criterion?"
In the best way, I counted for substitution of a root in the initial equation. For this purpose there is an easy alogritichesky way described in the article Value of a Derivative of a Polynomial by Horner's method. If expression addresses in zero, that is is true, then the sign does not change. If differently that a sign we put minus.
It is possible to solve the complex equations 4 degrees rather easily and quickly now. You will not find it in online services.
Try to solve the equation 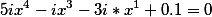
One of roots is equal
Who considers what the valid part can be neglected and rejected as "nearly zero" is deeply mistaken. Having rejected it we will have a value of function 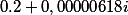
And only taking into account "such small" the valid part the equation to become identical. Therefore accuracy in calculations are very important. If you suddenly noticed an error in calculations (and suddenly?), the request to report. But I hope that it will not occur.
Several examples:
| Initial polynomial |
| Cubic rezolventa |
| Roots of a cubic rezolventa |
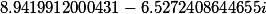 |
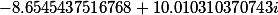 |
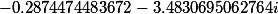 |
| Roots of the set polynomial 4 degrees |
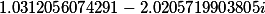 |
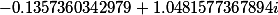 |
 |
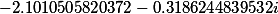 |
| Auxiliary coefficients |
F2=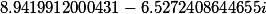 |
F1=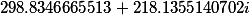 |
T=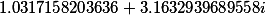 |
| Initial polynomial |
| Cubic rezolventa |
| Roots of a cubic rezolventa |
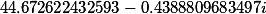 |
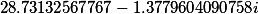 |
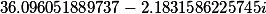 |
| Roots of the set polynomial 4 degrees |
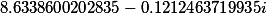 |
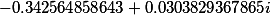 |
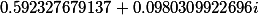 |
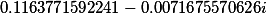 |
| Auxiliary coefficients |
F2=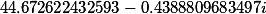 |
F1=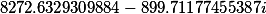 |
T=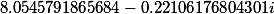 |



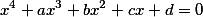

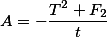
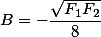
^2-\frac{F_1}{2}}{64})
=8B^2)
)