The calculator counts a greatest common divisor of two randomly given polynomials, through their coefficients. Polynomials may contain both expressions, and imaginaries.
| Initial polynom of f (x) (its coefficients) |
| We divide into the following polynom |
|
|
| First polynomial |
| Second polynomial |
| Remainders of division of two polynoms |
Calculation of the greatest common divisor (GCD) of two polynomials is considered. The principle which is used, same as well as for finding of GCD of usual numbers.
Difference of our calculator is that
1. It shows the intermediate remains at calculation
2. Polynomials can be complex, that is contain imaginary numbers.
The theory will not be any more, and at once we will pass to examples of calculation, and you will understand how it is calculated.
To find GCD of two polynomials
%20=%20x^{5}+x^{4}-4*x^{3}+5*x)
и
%20=%202*x^{3}-x^{2}-2*x+2)
At first we choose that polynom at which degree is higher also coefficient at this degree the greatest.
We divide one into other f(x) on g (x). It is possible to do it by hands and it is possible to use the calculator of division of a polynomial into a polynomial.
We receive the rest
*x^{2}+(0.5)*x+(3.5))
Now we divide already g(x) into the received rest
we receive
*x+(1.1358024691358))
Now we divide already g(x) into the received rest
we receive
We write out coefficients of polynoms at line dividing them a gap.
Received
1 1-4 0 5 it at us the first polynom
2 - 1 - 2 2 and it is the second
We enter them into the respective fields and we press to calculate.
We watch result
| First polynomial |
%20=%20x^{3}+(1-4)*x^{2}+(5)) |
| Second polynomial |
%20=%20(2)*x^{5}+(-)*x^{4}+%20x^{3}+(-)*x^{2}+(2)*x+(2)) |
| Remainders of division of two polynoms |
*x^{5}+(-)*x^{4}+%20x^{3}+(-)*x^{2}+(2)*x+(2))
|
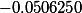
*x^{2}+(5))
*x^{2}+(12)*x+(-13))
*x+(3.0769230769228))
)