| Module (gap) rest (comma) Module (gap) rest, etc. |
|
|
| The received number |
One ancient Chinese task was:
"Find the number that, when divided by 3, gives the remainder of 2, when divided by 5, gives the remainder of 3, and when divided by 7, gives the remainder of 2"
To solve such problems, we will do the following
The source number from the source data can be expressed like this
Where k are integers
We write out the series changing k from 0 in increasing
It is easy to see that 23 is found in all three rows.
This is our answer, the next number (128) will meet only after 105 = 3 * 5 * 7 samples. Since these numbers are coprime, we simply take their product.
And so the general answer to our problem is
An easy algorithm to understand, isn't it?
But it is not entirely inconvenient when large numbers are encountered, and again, when composing the elements of a series, one can make a mistake.
There is another way
Let us be given a system of comparisons
Where 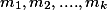
Let 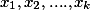
We can already solve such equations Comparisons of 1 degree. Number theory
Having learned these roots, we can calculate our initial number by the formula
For our example, the source data looks like this
Then the comparison system will have the form
Solving them we get
And our solution has the form
Or the same as
As you can see, the answer is the same.
Our bot solves such problems using the PHP GMP library. Therefore, to the accuracy of calculations and restrictions on the length of the values, this is for them :)
Although it has its own materials in particular: Calculation of the value of the Euler function , the remainder of the number in power modulo and the Diophantine equation with three unknowns
Important: It is logical and this should be taken into account when entering numbers, in a pair of numbers (module-remainder), the module (always!) Is larger than the remainder.
The second important point. The module is always (!) A positive number, the remainder can be negative, but it’s better to bring it to a positive number.
How to do it? All links to related materials have already been given.
Example
Find out what number is guessed if the remainder when dividing by 37 is 11, when dividing by 9 is 4, when dividing by 7 is 1, and when dividing by 100, the remainder is 25.
Note that the modules, that is, the numbers (37, 9, 7, 100) into which we divide the unknown number, are pairwise coprime. That is, we do not have a single pair of these numbers, so that they would have a common divisor.
If so, then we can solve a similar problem by the method described above. Enter in the input field
37 11, 9 4, 7 1, 100 25
In an instant we get the answer
| Received number |
mod(233100)) |
|
|



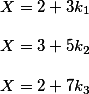
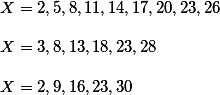
mod(105))
mod(m_1),%20&%20x=(c_2)mod(m_2),....,x=(c_k)mod(m_k))
mod(m_1)\\\\m_1m_3...m_kx_2=(1)mod(m_2)\\\\.........\\\\m_1m_2...m_{k-1}x_k=(1)mod(m_k))
mod%20(m_1m_2...m_k))
mod(3),%20&%20x=(3)mod(5),x=(2)mod(7))
mod(3)=1\\\\%20&%20(21x_2)mod(5)=1\\\\(15x_3)mod(7)=1)
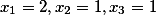
mod(3*5*7)=(233)mod(105))
mod(105)=(233-105-105)mod(105)=23mod(105))