| Whole positive number |
|
|
| Euler's function for the set number is equal |
The Euler function is such a function of a positive integer whose value is equal to the number of natural numbers less than a given number and mutually simple with it.
At the same time, it is believed that the number 1 is mutually simple with all natural numbers.
If the given number N is prime, it is logical to suggest that the Euler function is equal to N-1, since all numbers are less than N, are coprime to the given one.
For example, the value of the Euler function of 33 is 20. How did this happen?
Factor 33 into factors to get 3 * 11. Remember them and compare them with a number of numbers from 1 to 32.
Recall that mutually prime numbers are numbers that do not have common divisors.
We consider mutually prime numbers: 1,2, 3 (we do not take into account ) , 4,5, 6 (divisible by 3), 7,8, 9 , 10, 11 (divisible by 11), 12 , 13,14, 15 , 16 , 17, 18 , 19,20, 21 (divided by three), 22 (divided by 11), 23, 24 , 25,26, 27 , 28,29, 30 , 31,32
Let's calculate how many crossed out numbers have turned out?
There are 12 of them, a series of numbers contains 32 elements (from 1 to 33) then the number of non-crossed out (mutually prime) numbers will be 32-12 = 20
There is another easy way to calculate function values.
We decompose an arbitrary number such as 4832 into prime factors.
Get
Euler function is equal to
That is, if your number N is represented as simple factors of the form
then the Euler function will be equal
Here is another example
We calculate the value of the function of the number 100
then the value of the Euler function is
The applicability of the Euler number in number theory and cryptography is quite large, but we will use it to calculate linear Diophantine equations with two unknowns.
Good luck!



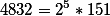
*(151^{1}-151^{0})=(32-16)(151-1)=2400)
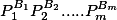
(P_2^{B_2}-P_2^{B_2-1}).....(P_m^{B_m}-P_m^{B_m-1}))
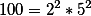
(5^{2}-5^{1})=(4-2)(25-5)=40)