| Elements of complex system of the linear equations |
|
|
| You entered the following system of the equations |
| Solution of system following |
Sets of linear equations are quite common in everyday calculations, so a great many methods have been invented to solve them. But before considering the simplest algorithm for finding unknowns, it is worth remembering what a system of such equations may have in general:
- have only one right decision;
- have an infinite number of roots;
- have an incompatible type (when there can be no solutions).
The Gauss method used by our ABAC bot is the most powerful and reliable tool for finding a solution to any system of linear equations.
Returning to the terms of higher mathematics, the Gauss method can be formulated as follows: using elementary transformations, the system of equations should be reduced to an equivalent system of triangular type (or the so-called step type), from which the remaining variables are gradually found, starting from the very last equation. With all this, elementary transformations over systems are exactly the same as elementary transformations of matrices in the arrangement for rows.
Our bot can instantly produce solutions to a system of linear equations with an unlimited number of variables!
The solution to such systems finds practical application in electrical engineering and geometry: calculating currents in complex circuits and deriving the equation of a straight line at the intersection of three planes, as well as in many specialized problems.
This service allows you to solve an unlimited in size system of linear equations with complex coefficients.
We calculate a complex system of linear equations of this form
%20\\%20%203^ix_0%20+%20(2+i)x_1%20-%20x_2%20&%20=%203%20\end{array})
| You have introduced the following system of equations |
%20\\%203%20\\%20\end{pmatrix}) |
| The system solution is as follows |
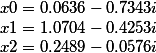 |
Good luck in the calculations!
|
|



%20\\%20%203^ix%20+%20(2+i)y%20-%20z%20&%20=%203%20\end{array})