| Partial fraction decomposition |
| Coefficients of a polynomial (numerator) through a gap |
| Poles/roots of a polynomial (denominator) through a gap |
|
|
| The set fractional and rational function |
| It is displayed for the sum of simple multipliers with the following coefficients |
In this article, the decomposition of a rational function into the sum of the simplest fractions will be considered and calculated.
The fractional rational function has the following form
For example, such
If the degree of unknown in the numerator is less than the degree of unknown in the denominator (as shown in the example), then such a function is called the correct fractional rational.
Each regular fractional rational function can be decomposed into the sum of the simplest fractions.
The simplest fraction has a general form
For example })
In almost every similar Internet resource, which discusses the decomposition of fractions, the method of uncertain coefficients is used as a solution method. We will not dwell on this method, since I do not want to produce another copy with slightly different text. We only recall that there it is necessary to solve a system of linear equations.
We will use a different technique, and the online calculator will also take this technique into service.
Source fraction
So, if we know all the roots of the denominator in our function, then we can convert
That is, we need to expand the function in the following form
and determine all unknown coefficients
We use the method (sometimes it is called the method of partial values), the practice of application is as follows:
Let x = 1 then substituting this value into the numerator we get the value 4, substituting the denominator without (x-1) we get (1 + 3) (1-7) (1 + 2) (1-2) = 72
Therefore, the coefficient
Now let x = -3. Then the numerator is (-3) ^ 2 + (- 3) + 2 = 8, and the denominator is (-3-1) (- 3-7) (- 3 + 2) (- 3-2 ) = 200
Therefore, the coefficient
Running through all x equal to 1, -3, 7, -2, 2, we calculate the coefficients
Our answer is
In my opinion, this solution is simpler. But this technique can be used when the denominator does not have multiple roots.
"How? Is such an easy way not applicable in the case of multiple roots?" - the reader exclaims distressedly.
Not everything is so bad really. Just in the case of multiple roots, for example, the ^3(x+3)(x-7)^2})
But for this you must be able to calculate the derivative of the polynomial, I hope you can do it.
First, convert the denominator to a polynomial. In order not to multiply manually, we use Create a polynomial at its roots
Let us introduce the roots of the denominator taking into account their multiplicity 1 1 1 -3 7 7
We get
We need to convert the initial fraction into this form
Based on the above example, we can immediately find out what the coefficients D, C and F are
Let's try to find out the coefficient B
Take the first derivative of the numerator. She is equal 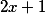
Substitute the unit there, divide by one factorial 1! = 1 and and remember the value = 3
Now the denominator. We find out the values of the derivatives of the denominator (for x = 1) through the online service. Value of a derivative of a polynomial by Horner's method
By entering the coefficients of the polynomial
we get the table
| Preset function | ||||||||||||||||
=x^{6}+(-14)*x^{5}+(43)*x^{4}+(92)*x^{3}+(-409)*x^{2}+(434)x+(-147)) |
||||||||||||||||
|
The first and second derivatives are equal to zero, but this is logical, since root 1 has a multiplicity of 3.
The value of the third derivative is 864
We make the equation
3 (this is the numerator I asked to remember) = B * 864/3! (Three factorials) + C * (- 288) / 4!
While for the majority it is not at all obvious what and where, but don’t worry, knowledge will come.
C we know and get an equation with one unknown
3 = B * 864 / 6-288 / 36/24
Let's find out what is the coefficient A.
We have almost everything
We take the second derivative of the numerator. It is equal to a constant number = 2
Divide into two factorial 2! = 2 and and remember the value = 1
Now we make the equation
1 = A * 864/3! + B * (- 288) / 4! + C (-960) / 5!
B and C are known to us.
I.e
I leave the value of the coefficient E for your homework, if the technique is of interest. If not, here is the answer
An online calculator that will do all this for you in automatic mode works, including in the field of complex numbers.
Now decomposing any correct fractional rational function into protozoa will not be the slightest difficulty.



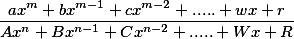
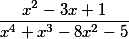
^d})
^5})

(x+3)(x-7)(x+2)(x-2)})
(x+3)(x-7)(x+2)(x-2)}=\frac{A}{(x-1)}+\frac{B}{(x+3)}+\frac{C}{(x-7)}+\frac{D}{(x+2)}+\frac{E}{(x-2)})
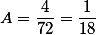
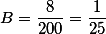
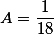
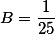


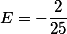
}%20+%20\frac{1}{18%20(x%20-%201)}%20-%20\frac{1}{27(x%20+%202)}%20+%20\frac{1}{25%20(x%20+%203)}%20+%20\frac{29}{1350%20(x%20-%207)})
*x^5+(43)*x^4+(92)*x^3+(-409)*x^2+(434)*x^1+(-147))
^3(x+3)(x-7)^2}==\frac{A}{(x-1)}+\frac{B}{(x-1)^2}+\frac{C}{(x-1)^3}+\frac{D}{(x+3)}+\frac{E}{(x-7)}+\frac{F}{(x-7)^2})
^2-3+2}{(-3-1)^3(-3-7)^2}=\frac{8}{-64*100}=-\frac{1}{800})
^2+1+2}{(1+3)(1-7)^2}=\frac{4}{4*36}=\frac{1}{36})
^3(7+3)}=\frac{58}{216*10}=\frac{29}{1080})
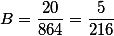
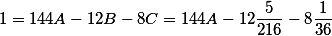
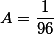
^3(x+3)(x-7)^2}=\frac{1}{96(x-1)}+\frac{5}{216(x-1)^2}+\frac{1}{36(x-1)^3}+\frac{-1}{800(x+3)}+\frac{E}{(x-7)}+\frac{29}{1080(x-7)^2})
