| Parameters of comparison of the first sort (through a gap) |
|
|
| The set equality |
| Will be true if x = |
In number theory, which deals with the study of integer values, there is another problem that we will try to solve.
if we know A, B, C then for what value of x this equality will be true?
As an example
The solution of such problems is inextricably linked with the Euler function . Although of course there is an alternative method of solution (according to Euclid), but we will not consider it.
How to solve such equations. Recall that, according to the Fermat-Euler formula, there is the following dependence. If a and m are coprime numbers (i.e. not having common divisors), then
Given that the Euler function of a prime m is m-1, we get the famous formula for any prime
where, as already mentioned, a must be coprime with m.
Euler’s method for solving similar comparisons in formulas looks like this
Then, solving the equation
find out what is x
Let's try to solve our first example.
the Euler function for 47 is 46
and the final formula is equal
If you count "looser" you get a huge number, but we need to find out only
To solve such a problem, we will use the material The number rest in degree on the module and find out that our solution
equally
check by substituting the resulting value
completely divided, which means our decision is right.
As you can see, we can also solve a similar problem along the way, which is called the inverse value modulo the residue class and which is expressed by the formula
Good luck!



mod(B)=C)
mod(47)=87)
}mod(m)=1)
=1)
}mod(m)=1%20=%3Ea*a^{\phi(m)-1}mod(m)=1)
-1}b)mod(m)=b)
mod(m)=b)
-1})
-1})
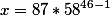
=%3Exmod(47))
=25)
}{(47)})
mod(B)=1)