| Point coordinate in the form of the x+iy form |
| ax+by+c=0 straight line coefficients through a gap |
| The set point with coordinates (X+Yi) |
| The set straight line |
| Coordinates of a mirror point |
Calculation of new coordinates of the set point or points which are specularly displayed concerning any set straight line is considered.
The algorithm for finding the coordinates of the mirror point is very simple
1. Determine the point of intersection of the abscissa axis and the line
2. Regarding this point, we make a rotation by an angle equal to the angular coefficient of the line.
How this is done can be found in the material turning points at an arbitrary angle
3. Using the view matrix 
4. Make a reverse turn (as in paragraph 2)
5. We get the result.
Mathematically, the solution of the problem is a product of three matrices, if the point around which the rotation is made is at the origin
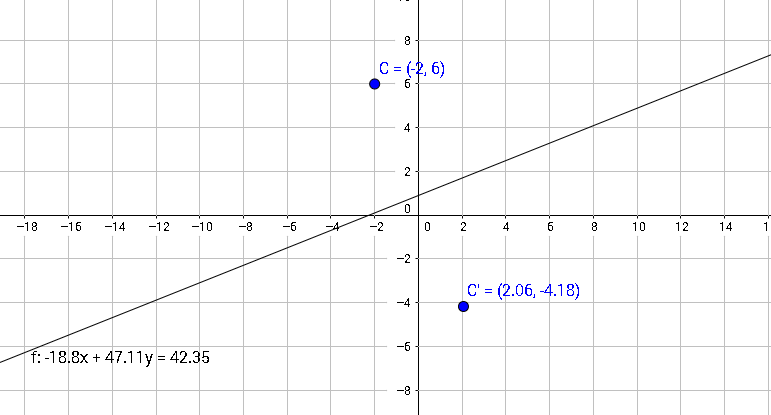
Consider the implementation of this algorithm using the example shown in the figure above.
So, we have a point with coordinates C (-2,6) and the equation of the line -18.8x + 47.11-42.35 = 0
Enter the data
The coordinates of point C are written here in this form -2 + 6i
The coefficients of the line are written through the space -18.8 47.11 -42.35
We get the answer
| Given point with coordinates (X: Y) |
 |
| Direct line |
*y+(-42.35)=0) |
| Mirror Point Coordinates |
 |
As you can see, this coincides with the graph at the beginning of the article made with geoGebra.
Good calculations !!



%20&%20sin(\phi)%20\\%20sin(\phi)%20&%20-cos(\phi)%20\end{pmatrix}*\begin{pmatrix}%20cos(\phi)%20&%20sin(\phi)%20\\%20-sin(\phi)%20&%20cos(\phi)%20\end{pmatrix})