Calculation of any number of a number of Fibonacci online

Serial number of a number of Fibonacci

Serial numbers and values of the next numbers of Fibonacci

For the first time, Fibonacci numbers appeared in the work "Liber abacci" ("The book about the abacus"), written by the famous Italian mathematician Leonardo from Pisa, who is better known by his nickname Fibonacci (Fibonacci - abbreviated filius Bonacci, i.e., son of Bonachchi). This book, written in 1202, came to us in its second version, which refers to 1228.

Almost at the time of the dark Middle Ages, this is the only book from Europe dated to the 13th century devoted to mathematics.

Liber abacci is a voluminous work that contains almost all the arithmetic and algebraic information of the time and played a prominent role in the development of mathematics in Western Europe over the next several centuries.

In particular, it was from this book that Europeans became acquainted with Hindu (“Arab”) figures.

The material reported in Liber abacci is explained on a large number of tasks, which constitute a significant part of this treatise.

Consider one such problem, placed on pages 123 -124 of the manuscript of 1228.

"How many pairs of rabbits are born in one year from one pair?"

“Someone placed a pair of rabbits in a place fenced on all sides by a wall to find out how many pairs of rabbits will be born during the year, if the nature of the rabbits is such that in a month a pair of rabbits gives birth to another pair, and rabbits give birth from the second month after his birth. Since the first pair in the first month gives birth, double, and this month there will be 2 pairs; of these, one pair, namely the first, gives birth in the next month, so that in the second month there are 3 pairs; of these, in the next month 2 pairs will give birth, so in the third month 2 more pairs of rabbits will be born, and the number of pairs of rabbits in this month will reach 5; 3 pairs of them will give birth in the same month, and the number of pairs of rabbits in the fourth month will reach 8; 5 of them will produce another 5 pairs. which, combined with 8 couples, will produce 13 couples in the fifth month: of which 5 couples born this month do not give offspring in the same month, and the remaining 8 couples give birth, so that in the sixth month there are 21 couples; stacked with 13 couples who are born in the seventh month, they give 34 couples; stacked with 21 pairs born in the eighth month, they give 55 pairs this month; stacked with 34 couples born in the ninth month, they give 89 couples; stacked again with 55 pairs that are born in the tenth month, they give 144 pairs this month; again stacked with 89 pairs that are born in the eleventh month, they give 233 pairs this month; stacked again with 144 couples born in the last month, they give 377 couples; so many pairs were produced by the first pair at a given location by the end of one year. Really. in these fields you can see how we do it; namely, we add the first number to the second, that is, 1 and 2; and the second with the third; and third with fourth; and fourth and fifth; and so one by one. until we add the tenth to the eleventh, that is, 144 to 233; and we get the total number of rabbits mentioned, that is, 377; and so it can be done in order to an infinite number of months "

As we can see, the following sequence is obtained: 1, 1, 2, 3, 5, 8.13, 21.34 ..., in which each number, starting from the third, is the sum of the two previous ones.

It was such a sequence that was called Fibonacci numbers

Fibonacci numbers arise in a wide variety of areas of life.

On a sunflower, the seeds are arranged in spirals, and the number of spirals going in one direction and the other is different - they are consecutive Fibonacci numbers (for example, spirals can be 34 and 55).

The same is observed on the fruits of pineapple, where there are usually 8 spirals.

Fibonacci numbers 3, 5, 8, 13 appear in a curious geometric sophism, claiming that “64 = 65” or “lost area” by cutting the square 8X8 and folding a rectangle 5X13 from it.

Fibonacci numbers also arise when describing a winning strategy in the ancient Chinese game of "dzyanypitszy", in which two players take turns taking stones from two piles: either an arbitrary amount from one pile, or equally from two (the player who takes the last stone wins).

It was found that fractions of the a / c type corresponding to the helical arrangement of leaves on the plant stem are often the ratios of successive Fibonacci numbers.

For beech and hazel, this ratio is 2/3, for oak and apricot - 3/5, for poplar and pear - 5/8, for willow and almond - 8/13, etc.

Fibonacci numbers were inextricably linked with the so-called "golden ratio", which was used and practically erected in a kind of "cult" by the ancient Greeks.

The golden ratio is the division of an arbitrary segment in such a way that most refers to the smaller, just as the entire segment refers to the larger.

Figures, paintings, buildings and everything that surrounds us, according to the ancients, everything should obey the "golden ratio". The correctness of this ratio indicates the external harmony of the observed object.

If we want to solve the problem and determine in numbers what the golden ratio is, we need to solve the proportion

$golden ratio$

If we take the smaller part of b as unity, and denote a by x, we get

$golden ratio formula$

$x ^ 2-x-1 = 0$

The solution of this equation gives us the following result

$x = \ frac {1- \ sqrt {5}} {2}$

A positive number equal to 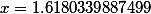$x = 1.6180339887499$ and there is a golden ratio

The most surprising thing is that despite the obvious irrationality of the resulting number, it is the “golden section” that will help us find an arbitrary number of the Fibonacci series. To do this, we use the so-called Binet formula:

$F_n = \frac{\left(\frac{1 + \sqrt{5}}{2}\right)^n - \left(\frac{1 - \sqrt{5}}{2}\right)^n}{\sqrt{5}}$

This formula is used by the bot to give you an exact answer.

And also about the "golden section". Let's try to translate the number 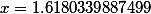$x = 1.6180339887499$ in a chain or in another, continuous fraction. To do this, use the bot Continuous, continued fractions online

We will see that the irrational number $x = \ frac {1- \ sqrt {5}} {2}$ has a beautiful, in its beauty, continuous fraction.

$continuous fraction of the golden ratio$

The sum of the Fibonacci series

If we carefully look at the Fibonacci series 1, 1, 2, 3, 5, 8.13, 21.34, we will notice another feature.

The sum of the Fibonacci series is equal to the number of this series increased by two positions minus two.

For example, what is the sum of the first six numbers of this series 1 + 2 + 3 + 5 + 8 + 13?

It is equal to the eighth (six + two) Fibonacci numbers minus 2. that is 34-2 = 32

Thus, in order to calculate the sum of a series, it is not necessary to use cycles or to sum each element, it suffices to find the Fibonacci number, whose number is two more from the given value and subtract two by the Binet formula.

Syntax

Jabber: fb <number>

WEB: <number>

A number can be an integer that denotes a sequence number in a Fibonacci series.

0,1,1,2,3,5,8 ......

Examples

Example:

Define the 30th number of the series

fb 30

we get the answer

The 30th number of the Fibonacci series is 1346269

The following numbers in this series are equal

The 31st number is 2178309

32nd number equals 3524578

33rd number is 5702887

34th number is 9227465

The 35th number is 14930352

36th number is 24157817

37th number equals 39088169

38th number equals 63245986

39th number is 102334155

Calculation of any number of a number of Fibonacci online

The sum of the Fibonacci series

Syntax

Examples

Most popular articles