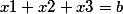Creating a polynomial (polynomial) of one variable online

You have entered the following polynomial roots

The resulting polynomial with given roots has the form

Description

Often in life a situation arises that is inverse to the problem of finding the roots of a polynomial of the form

where b,c....z,w are the coefficients of the polynomial.

When n=2 we get a quadratic equation

for n=3 cubic, etc.

This service allows you to solve the problem of finding such coefficients if the roots of this polynomial are known.

It seems like a simple task, but when creating a fourth-degree polynomial, calculating the elements of the polynomial is already quite difficult.

See for yourself.

Let's take a quadratic equation 

Let us know its roots   and 

Then  ,    

It is calculated simply and, moreover, based on these two rules, you can calculate verbally (in your head) integer roots for integer elements of a quadratic equation.

You just need to factor it    into two factors so that their sum is equal 

These factors will be the roots of the quadratic equation.

Now consider the cubic equation

Let us know its roots   ,   and 

Then  

It's already more difficult. If we take a polynomial of degree 4 and higher, we will see that the complexity of calculating the elements of the polynomial increases in geometric progression.

It will be even more difficult if the known roots contain complex numbers.

It is to simplify such calculations that this bot was invented.

In the examples you will see how easily and simply the bot creates a polynomial of arbitrary degree using known roots.

Examples

Determine the coefficients of a polynomial when the following roots are known

1 2+i 2-i

You have entered the following polynomial roots

The resulting polynomial with given roots has the form