| Algebraic form of complex number |
|
|
| 1. We determine the module of complex number by a formula \(\sqrt{x^2+y^2}\) |
| 2. We determine an argument by a formula \(\phi=atan(\frac{y}{x})\) in radians and degrees |
Since the moment when imaginary numbers began to be used in the solution of the cubic equations, to complex numbers treated as the unloved, but rich relative. "Well, helps money, but it is such. such, fie."
The situation was developed by 180 degrees when each complex number was simply presented in the form by points on the Cartesian plane.
It turned out that "relative" not and is bad, and he has a mass of advantages and different useful properties.
We will tell you about one of these properties.
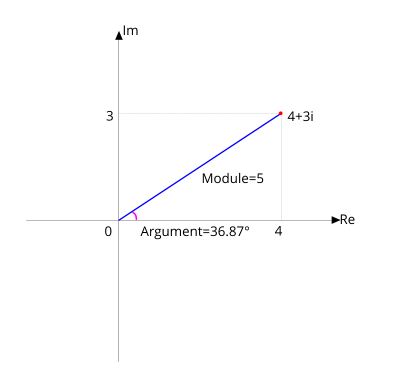
As you see on the screen, any point on the Cartesian plane can be presented as the line (it is designated blue in color) having two parameters (the direction and length)
In geometry it is called - transformation from the Cartesian system to polar system of coordinates.
During the work with complex numbers look number \(x+ib \) (\(4+3i \)) - is called representation in an algebraic look, and \(m*e^ { i\phi}\) \(5e^ { i36.87 ° }\) - in an indicative look.
The module is calculated on Pythagorean theorem \(\sqrt { x^2+y^2}\), and an argument through арктангес \(\phi=atan (\frac {y} {x}) \)
From an indicative look in algebraic we already have a converter.
|
|


