| Алгебраическая форма комплексного числа |
| 1. Определяем модуль комплексного числа по формуле \(\sqrt{x^2+y^2}\) |
| 2. Определяем аргумент по формуле \(\phi=atan(\frac{y}{x})\) в радианах и градусах |
C момента, когда мнимые числа начали использоваться в решении кубических уравнений, к комплексным числам относились как к нелюбимому, но богатому родственнику. "Ну да, помогает деньгами, но ведь он такой.. такой, тьфу.."
Ситуация развернулась на 180 градусов, тогда, когда каждое комплексное число просто представили в виде точки на декартовой плоскости.
Оказалось, что "родственник" не так и плох, и у него есть масса достоинств и разных полезных свойств.
Об одном из этих свойств мы вам расскажем.
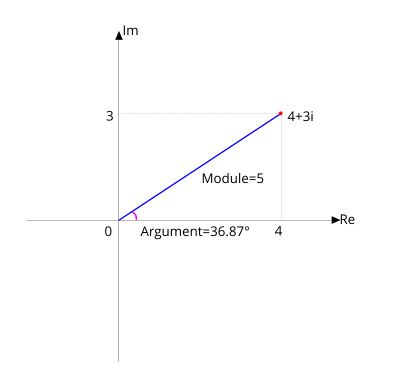
Как Вы видите на экране, любую точку на декартовой плоскости можно представить как линию ( обозначена синем цветом) обладающая двумя параметрами ( направлением и длиной)
В геометрии это называется - преобразование из декартовой системы в полярную систему координат.
При работе с комплексными числами число вида \(x+ib\) (\(4+3i\))- называется представлением в алгебраическом виде, а \(m*e^{i\phi}\) (\(5e^{i36.87°}\)) - в показательном виде.
Модуль высчитывается по теореме Пифагора \(\sqrt{x^2+y^2}\), а аргумент через арктангес \(\phi=atan(\frac{y}{x})\).
Конвертер из показательного вида в алгебраический у нас уже есть.













