When working with matrices, it is never superfluous to know about their basic properties. Sometimes it helps to unambiguously determine the determinant of the matrix without resorting to automatic calculations, such as Calculating the determinant of a complex matrix online
Property 1
The value of the determinant will not change if all its rows are replaced by columns, and each row is replaced by a column with the same number, i.e.

Property 2
The permutation of two columns or two rows of the determinant is equivalent to multiplying it by -1.

Property 3
If the determinant has two identical columns or two identical rows, then it is equal to zero.
Property 4
Multiplying all elements of one column or one row of the determinant by any number k is equivalent to multiplying the determinant by this number k.

Property 5
If all elements of a column or a row are equal to zero, then the determinant itself is equal to zero. This property is a special case of the previous one (for k = 0 ).
Property 6
If the corresponding elements of two columns or two rows of the determinant are proportional, then the determinant is zero. This is a consequence of two properties 4 and 3.
Property 7
If each element of the n-ro column or nth row of the determinant is the sum of two terms, then the determinant can be represented as the sum of two determinants, of which one in the nth column, or respectively in the nth row, has the first of mentioned terms, and the second - the second; the elements standing in the remaining places are the same for all three determinants.

Property 8
If we add to the elements of a column (or some row) the corresponding elements of another column (or another row) multiplied by any common factor, then the value of the determinant will not change.

Further properties of the determinants are associated with the concept of algebraic complement and minor.
The minor of a certain element is the determinant obtained from this element by deleting the row and column at the intersection of which this element is located.
The algebraic complement of any element of the determinant is equal to the minor of this element, taken with its sign, if the sum of the row and column numbers at the intersection of which the element is located is an even number, and with the opposite sign if this number is odd.
In this article, we will denote the algebraic complement of an element by a capital letter of the same name and the same number as the letter that designates the element itself.
Property 9
Determinant

equal to the sum of the products of the elements of any column (or row) by their algebraic additions /
In other words, the following equalities hold:

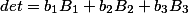
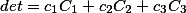
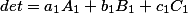
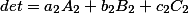
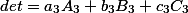
There is another interesting property of the matrix determinant in the matrix determinant material . Alternative look.


