Работая с матрицами, никогда не лишне знать об их основных свойствах. Иногда это помогает однозначно определить детерминант матрицы, не прибегая к автоматическим расчетам, наподобие Расчет определителя комплексной матрицы онлайн
Свойство 1
Величина определителя не изменится, если все его строки заменить столбцами, причем каждую строку заменить столбцом с тем же номером, т. е.

Свойство 2
Перестановка двух столбцов или двух строк определителя равносильна умножению его на -1.

Свойство 3
Если определитель имеет два одинаковых столбца или две одинаковые строки, то он равен нулю.
Свойство 4
Умножение всех элементов одного столбца или одной строки определителя на любое число k равносильно умножению определителя на это число k.

Свойство 5
Если все элементы некоторого столбца или некоторой строки равны нулю, то сам определитель равен нулю. Это свойство есть частный случай предыдущего (при k = 0).
Свойство 6
Если соответствующие элементы двух столбцов или двух строк определителя пропорциональны, то определитель равен нулю. Это следствие двух свойств 4 и 3.
Свойство 7
Если каждый элемент n-ro столбца или n-й строки определителя представляет собой сумму двух слагаемых, то определитель может быть представлен в виде суммы двух определителей, из которых один в n-м столбце, или соответственно в n-й строке, имеет первые из упомянутых слагаемых, а другой — вторые; элементы, стойящие на остальных местах, у всех трех определителей одни и те же.

Свойство 8
Если к элементам некоторого столбца (или некоторой строки) прибавить соответствующие элементы другого столбца (или другой строки), умноженные на любой общий множитель, то величина определителя при этом не изменится.

Дальнейшие свойства определителей связаны с понятием алгебраического дополнения и минора.
Минором некоторого элемента называется определитель, получаемый из данного путем вычеркивания строки и столбца, на пересечении которых расположен этот элемент.
Алгебраическое дополнение любого элемента определителя равняется минору этого элемента, взятому со своим знаком, если сумма номеров строки и столбца на пересечении которых расположен элемент, есть число четное, и с обратным знаком, если это число нечетное.
В данной статье, алгебраическое дополнение элемента мы будем обозначать большой буквой того же наименования и тем же номером, что и буква, которой обозначен сам элемент.
Свойство 9
Определитель

равен сумме произведений элементов какого-либо столбца (или строки) на их алгебраические дополнения/
Иначе говоря, имеют место следующие равенства:
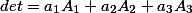
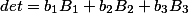
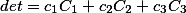
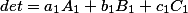
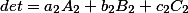
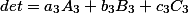
Есть еще одно интересное свойство определителя матрицы в материале Определитель матрицы. Альтернативный взгляд.













