ФСР онлайн. Фундаментальное решение системы уравнений

Каждое уравнение или переносится на новую строку или разделяется точкой с запятой4 1 1 31 27 -12;5 6 1 47 47 -23;8 7 6 92 85 -58

Исходная система уравнений

Фундаментальная система решений (ФСР) данной системы уравнений

База системы/знаменатель

 

Попробуем решить систему уравнений, типа

Решение подобных систем неразрывно связывают с формулой приведения матрицы к треугольному виду. Это наглядно, красиво и никогда не дает сбоев.  Есть только одно но, нужно делать очень много ручной работы и использовать понятия ранга матрицы

Нет никаких сомнений подвергать выверенную веками технологию, но есть не менее красивое решение используя векторное произведение. Информации по ним на январь 2019 года в интернете нет, поэтому скромно назовемся первооткрывателем.

Это решение конечно же не оптимально (по быстродействию), так как при вычислении векторного произведения, надо вычислять определитель матрицы, а это так или иначе  вычисление треугольной матрицы.

Но решение красиво и наглядно, кроме этого легко видеть критерий при котором система не имеет решений.

В чем же суть методики?

Решая эту систему как произведение двух векторов, мы получим

А следоватетельно, корни системы равны 

Для тех кто не верит, это легко проверяется подстановкой

Такой же нехитрый прием используется  и при системах где количество переменных может быть и пять и десять.

Рассмотрим, как же решаются такие системы с помощью векторных произведений.

Итак, у нас есть исходная система

Приведем её вот в такой вид

У нас получилось 6 столбцов.

На этом этапе не будем вводить новых сущностей и не используем в своей работе понятия ранга матрицы. Мы просто видим что уравнений 3, а переменных 5-ть. Следовательно общее решение будет использовать 5-3=2 независимых переменных.

На этом же шаге, мы можем определить, какие же из переменных будут свободными. Так как фантазии ноль, то те из переменных, которые будут правее всех, те  и станут свободными.

То есть свободными у нас будут две переменных 

А теперь за три шага определяем фундаментальное решение исходной системы

Шаг1.

Шаг 2.

Шаг 3.

Нет необходимости подробно рассказывать откуда  мы берем данные. Это очевидно

Интереснее то, что мы с этими "векторами" делать будем.

Разделим их на -81

получаем следующие три вектора

Таким образом фундаментальное решение  принимает вид

Великолепно! Не правда ли....

Хочется еще что то решить.... Еще один пример

Это интересное уравнение, так вектора в любом сочетании будут давать ноль.

Это говорит нам о том, что одно из уравнений "лишнее". Согласимся с этим и уберем его. Например последнее.

Тогда нам надо выбрать две свободных переменных, пусть это будут переменные с индексами 2 и 4.

Тогда вектора находятся как

Разделим на -3 и наше общее решение будет иметь вид

Не каждому сразу становиться ясно откуда у нас появляются нули и единицы в нашем стройном вектором ряде.  Это  связано с тем, что мы свободные переменные выбрали как нашей душе угодно, а не самые крайние правые. 

Если бы мы взяли переменные с индексами 3 и 4  как свободные то решение бы мы переписали так как нам бы выдала машина.

В начале статьи мы упомянули о критерии неразрешимости той или иной системы уравнений. В классической версии для этого исползуется правило Кронекера-Копелли, здесь же просто анализируется результат векторного произведения.

Если результирующий вектор имеет вид 

где 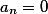, а среди всех оставшихся есть хотя бы один не нулевой, то такая система решений не имеет

Примеры, неразрешимых систем уравнений

Если результирующий вектор имеет все нулевые коэффициенты ( мы такой пример рассмотрели выше), то это говорит о том, что или как минимум одно из уравнений есть линейное представление другого, и/или одна из переменных  пропорциональна другой.

Калькулятор, представленный здесь, дает Вам возможность самому проанализировать исходную систему, за Вас он лишь сделает точные расчеты, по тем данным, что Вы ему введете.

Вот один из примеров

 

Исходная система уравнений

Фундаментальная система решений (ФСР) данной системы уравнений

База системы/знаменатель