| Коэффициенты многочлена разделенные пробелами |
| Коэффициент C в биноме вида x-C |
|
|
| Заданный многочлен имеет вид |
| если разделим его |
| Получим многочлен |
| и остаток |
=a_0x^{n}+a_1x^{n-1}+a_2x^{n-2}+.....+a_{n-1}x+a_n)
на бином вида
результат деления есть функция вида
=b_0x^{n-1}+b_1x^{n-2}+b_2x^{n-3}+.....+b_{n-2}x+b_{n-1})
Такой результат получается только в результате деления исходного многочлена на бином без остатка.
В общем же случае говорится, что функцию )
=q(x)(x-c)+r)
где r - это остаток от деления.
Коэффициенты функции )
Схема Горнера очень удобна своей простой и отсутствием функции деления. Это позволяет решать с повышенной точностью подобные уравнения, а также решать целочисленные уравнения, без каких либо машинных(компьютерных) погрешностей.
Кстати!
Есть новый калькулятор который осуществляет деление многочлена на многочлен с остатком . Работает в том числе и в комплексном поле, кроме того, делящий многочлен может быть на самом деле многочленом(!), а не биномом, как в этой статье.
Кроме этого, эта же схема позволяет решать задачу определения значения функции при каком либо значении. "Фи!" - скажете Вы. "Это же элементарно, любой калькулятор это может".
Да конечно, поставив вместо неизвестного x необходимое значение мы получим нам нужный результат, но какой ценой?
Нам придется возводить значения в степень, что несомненно внесет свою погрешность в расчеты.
Это явно проявляется при работе в поле комплексных чисел, при делении многочлена на комплексный бином.
Нам проще воспользоватся теоремой Безу, которая гласит: Остаток r от деления многочлена на 
Бот созданный на этом сайте, позволяет Вам решать поставленную задачу методом Горнера, не только для действительных чисел, но и для комплексных. Это расширяет возможности применения бота и позволяет более полно исследовать функцию.
Если делящий многочлен не является одночленом, то стоит воспользоваться калькулятором который делит произвольные многочлены друг на друга с вычислением остатка
Теперь рассмотрим примеры.
=2x^3-3x+2)
Пишем коэффициенты 2 0 -3 2 и через точку запятой -2. Надеюсь понятно почему пишем -2, а не+2 ?
Получаем ответ
| Заданный многочлен имеет вид |
=(2)*x^3+(-3)*x^1+(2)) |
| если разделим его |
) |
| Получим многочлен |
=(2)*x^2+(-4)*x^1+(5)) |
| и остаток |
 |
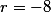Следующий пример исходный полином тот же, но значение С будет комплексным например 1+i
Пишем коэффициенты 2 0 -3 2 и через точку запятой 1+i
Получаем
| Заданный многочлен имеет вид |
|
| если разделим его |
) |
| Получим многочлен |
=(2)*x^2+(2+2i)*x^1+(-3+4i)) |
| и остаток |
 |
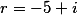Таким образом мы можем писать любые значения, в том числе и комплексные, в коэффицентах как делимого полинома так и делящего бинома
Удачных расчетов!