| Новые координаты полученные при повороте фигуры(точки) на заданный угол |
|
Произвольный поворот координат вокруг точки
Поворот - это движение фигуры в пространстве вокруг неподвижной точки, принадлежащей этому же пространству.
Возникают задачи, как определить новые координаты какой либо фигуры при повороте на произвольный угол, относительно произвольной точки.
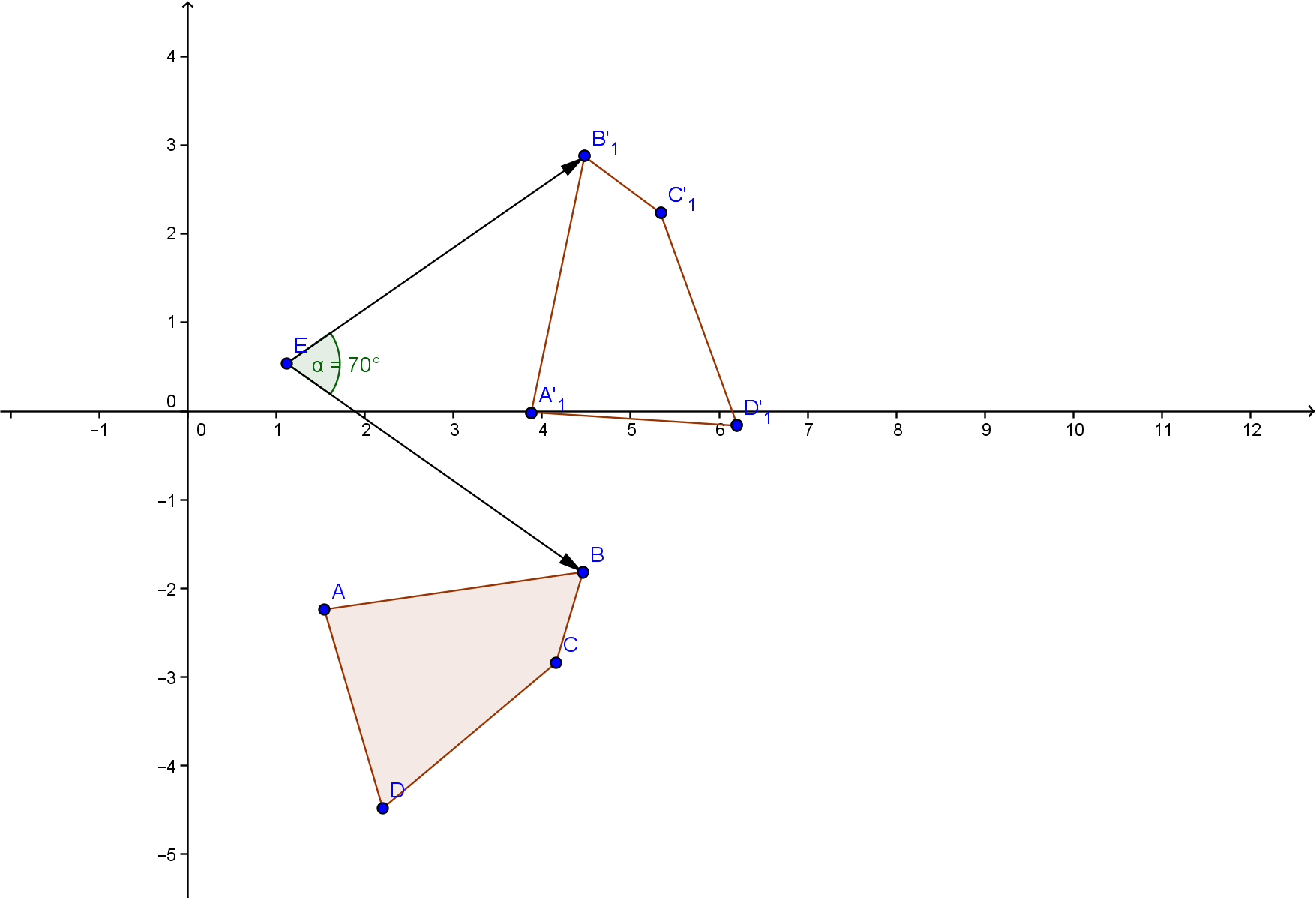
На данном рисунке отобразено поворот фигуры на угол в 70 градусов против часовой стрелки относительно точке Е.
Есть два представления расчета новых координат при решении подобных задач.
Фигура ABCD имеет следующие координаты вершин A=(1.54:-2.24) B=(4.46:-1.82) C=(4.16:-2.84) D=(2.2:-4.48)
точка E=(1.12:0.54) вокруг которой и будет происходить вращение
Алгоритм определения новых координат
Пример будем рассчитывать только для одной точки, так как для остальных точек весь процесс одинаков
1. Приведем начало координат к точке E. То есть точка E будет с координатами (0:0) а точка A (1.54-1.12:-2.24-0.54)
A=(0.42:-2.78)
2. Высчитаем новые координаты точки A1 по следующим формулам
где f - угол поворота. Хотелось бы обратить Ваше внимание на то, что не надо высчитывать синус или косинус 70 градусов "в лоб", как иногда захочется сделать.
Общепринятно, что все расчеты тригонометрических функций осуществляются в радианах.
Поэтому сначала угол 70 градусов приводим к радианам по формуле =1.22173047639603)
А вот теперь считаем по выше указанным формулам, новые координаты.
3. получаем новые координаты точки A=(2.76:-0.56)
4. делаем обратные действия, которые делали в шаге первом, то есть возвращаем начало координат туда, куда и положено
тогда окончательная точка А имеет координаты (2.76+1.12:-0.56+0.54) => (3.88:-0.02)
Преобразовываем таким образом все остальные точки фигуры.
Второе представление в виде умножения матриц.
Координаты точки A представляют в виде вектора
и умножают на матрицу следующего вида
которая называется матрицей поворота
Результат - новые координаты точки.
Используется в построении и моделировании. Развивает пространственное ориентирование, помогает решать сопутствующие задачи в геометрии, алгебре, физике.
Синтаксис
Для тех, кто пользуется XMPP клиентами: rot <координаты>;<поворот в градусах>;<точка вращения>
Координаты - строка, содержащая координаты в виде x:y (где x - абсцисса координаты, y - ордината координаты), разделенные хотя бы одним пробелом
Точка вращения - точка, относительно которой будет осуществляться поворот, всех заданных координат.
Поворот в градусах - поворот фигуры на заданный угол. Если число положительное - то поворот производится ПРОТИВ часовой стрелке, если отрицательный, то ПО часовой стрелке.
Примеры
Пример: задан треугольник следующими координатами A(1:1) B (5:5) C(0:7)
Необходимо повернуть треугольник на 30 градусов против часовой стрелки относительно точки с координатами 3:3
Тогда запрос будет выглядеть так
rot 1:1 5:5 0:7;30;3:3
и получаем следующее
Новые координаты при повороте на угол 30
Относительно координаты 3:3
A (2.2679491924311 : 0.26794919243112)
B (3.7320508075689 : 5.7320508075689)
C (-1.5980762113533 : 4.9641016151378)
Самое приятное в том, что с помощью Построить график функции c помощью GeoGebra Вы можете сами нарисовать этот треугольник и повернуть его на тот же самый угол. И это будет отображено не только в численной виде, но и в графическом.
А это совсем другой уровень восприятия, и возможность использования этой графики в своих работах, дипломных или аттестационных не может не радовать.
-ysin(\phi))
+ycos(\phi))
=1.22173047639603)

 & -sin(\phi) \\ sin(\phi) & cos(\phi) \end{pmatrix})
 & -sin(\phi) \\ sin(\phi) & cos(\phi) \end{pmatrix})













