Косинусоидальный импульс при произвольном угле отсечки

Параметры косинусоидального сигнала

Угол отсечки (в градусах)

Номер коэффициента

Коэффициент постоянной составляющей

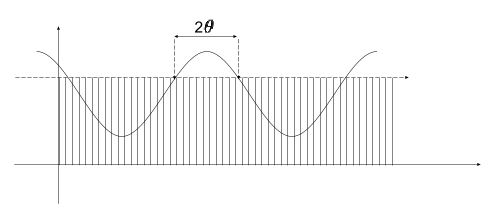
В радиотехнике часто приходится иметь дело с импульсами косинусоидальной формы.

То есть это не обычное гармоническое колебание, а очень на него похожее в какие то периоды времени.

У такого сигнала выделяют два основных параметра: максимальное значение импульса и величина угла отсечки.

Углом отсечки $\theta$ называется выраженная в дуговой или градусной мере половина отрезка времени, в течении которого в цепи существет ток, изменяющийся по закону верхушки косинусоиды(синусоиды)

При разложении такого сигнала, обычно интересуются значениями коэфициентов разложения, то есть отношениями амплитуд гармоник к максимальному значению импульса.

Коэффициент постоянной составлляющей

$a_0=\frac{I_0}{I_max}=\frac{sin\theta-\theta{cos\theta}}{\pi(1-cos\theta)}$

Коэффициент первой гармоники

$a_1=\frac{I_1}{I_{max}}=\frac{2\theta-sin\theta}{2\pi(1-cos\theta)}$

Коэфициент второй гармоники

$a_2=\frac{I_2}{I_{max}}=\frac{sin2\theta{cos\theta}-2cos2\theta{sin\theta}}{3\pi(1-cos\theta)}$

Коэфициент третьей гармоники

$a_3=\frac{I_3}{I_{max}}=\frac{sin3\theta{cos\theta}-3cos2\theta{sin\theta}}{12\pi(1-cos\theta)}$

В общем случае коэфициент k гармоники можно выразить так

$a_k=\frac{I_k}{I_{max}}=2\frac{sink\theta{cos\theta}-cosk\theta{sin\theta}}{k\pi(k^2-1)(1-cos\theta)}$

Полученную функцию еще иногда называет функциями Берга.

Отношение первой гармоники к постоянной составляющей

$\frac{a_1}{a_0}=\frac{2\theta-sin2\theta}{2(sin\theta-\theta{cos\theta})}$

если мы будем раскладывать косинусоидальный импульс в ряд Фурье то получим следующий ряд

$f(x)=\frac{A}{\pi(1-cos\theta)}*((sin\theta-\theta{cos\theta})+(\theta-sin\theta{cos\theta})cosx+....+[\frac{sin(n+1)\theta}{n+1}+\frac{sin(n-1)\theta}{n-1}-\frac{2sin\theta{n}cos\theta}{n}]cosn\theta$

Калькулятор позволяет рассчитывать значения функций Берга, при заданных параметрах.

Количество гармоник по умолчанию , всего пять, но они "плавающие". То есть можно рассчитать с 1 по 5 гармонику, можно рассчитать с 12 по 17 гармонику, и так далее.

Примеры расчета

Рассчитать первые 5 коэффициентов при угле отсечки равной 20 градусов

Коэффициент постоянной составляющей
0.073923
Коэфициент 1 гармоники
0.146057
Коэфициент 2 гармоники
0.140781
Коэфициент 3 гармоники
0.132291
Коэфициент 4 гармоники
0.121019
Коэфициент 5 гармоники
0.107531