В этом новом для сайта направлении мы будем рассматривать разложение в ряд Фурье, периодических несинусоидальных функций.
Разложение в ряд
=f[\omega(t+T)])
или
можно разложить в ряд синусоидальных функций
где

)


Чаще ряд Фурье изображается в виде двойного ряда синусов и косинусов, которые в начале координат не имеют сдвига фаз:
В этих формулах
Если кривая симметрична относительно оси абсцисс (х), считая от начала первой и второй половины периода, то в разложении отсутствуют постоянная составляющая и гармоники четных порядков.
=A_1sin(x)+A_3sin(3x)+A_5sin(5x)+.....)
 .. могут быть положительными или отрица¬тельными величинами.
.. могут быть положительными или отрица¬тельными величинами.Сигнал в виде трапеции
Функция разложения в ряд Фурье будет иметь вид
Сигнал в виде прямоугольника
Функция разложения в ряд Фурье будет иметь вид
Сигнал в виде равнобедренного треугольника cимметричного оси абсцисс
Функция разложения в ряд такого сигнала будет иметь вид
СИГНАЛ В ВИДЕ РАВНОБЕДРЕННОГО ТРЕУГОЛЬНИКА
Функция разложения в ряд такого сигнала будет иметь вид
Сигнал в виде прямоугольного треугольника (первый вариант)
Функция разложения в ряд такого сигнала будет иметь вид
Сигнал в виде прямоугольного треугольника (второй вариант)
Функция разложения в ряд такого сигнала будет иметь вид
Сигнал в виде пилоообразной кривой
Функция разложения в ряд Фурье такого сигнала будет иметь вид
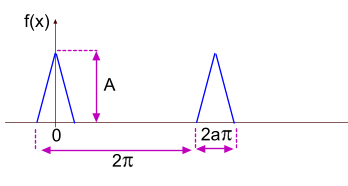
Сигнал в виде короткого прямоугольного импульса
Функция разложения в ряд Фурье такого сигнала будет иметь вид
Сигнал в виде короткого треугольного импульса
Функция разложения в ряд Фурье такого сигнала будет иметь вид
=A[\frac{\alpha}{2}+\sum_{n=1}(\frac{2}{n\pi}sin(n\pi\alpha)-\frac{2}{\pi^2n^2\alpha}(n\pi\alpha{sin(n\alpha\pi)}-2sin(\frac{n\alpha\pi}{2})^2))cos(nx)])














=f(\alpha+2\pi))
=A_0+A_1sin(t\omega+\psi_1)+A_2sin(2t\omega+\psi_2)+A_3sin(3t\omega+\psi_3)+.....)
=A_0+B_1sin(x)+B_2sin(2x)+B_3sin(3x)+.....+C_1cos(x)+C_2cos(2x)+C_3cos(3x)+.....)



,\frac{C_2}{B_2}=tan(\psi_2),\frac{C_3}{B_3}=tan(\psi_3).....)
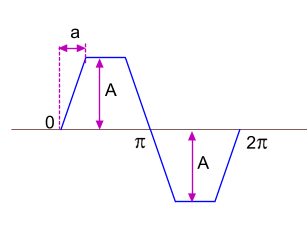
=\frac{4A}{\alpha\pi}(sin(\alpha)sin(x)+\frac{1}{3^2}sin(3\alpha)sin(3x)+\frac{1}{5^2}sin(5\alpha)sin(5x)+....))
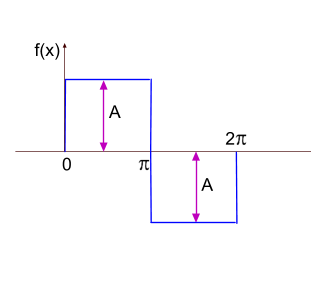
=\frac{4A}{\pi}(sin(x)+\frac{1}{3}sin(3x)+\frac{1}{5}sin(5x)+....))
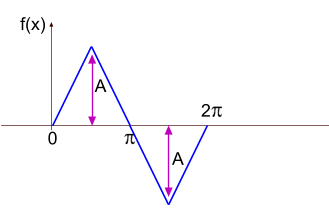
=\frac{8A}{\pi^2}(sin(x)-\frac{1}{3^2}sin(3x)+\frac{1}{5^2}sin(5x)-....))
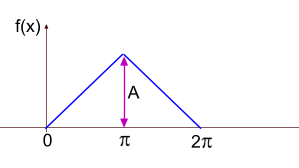
=\frac{A}{2}-\frac{4A}{\pi^2}(cos(x)+\frac{1}{3^2}cos(3x)+\frac{1}{5^2}cos(5x)+....))
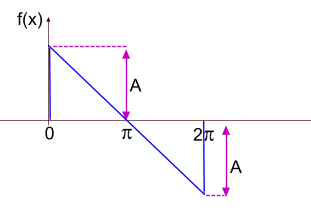
=\frac{2A}{\pi}(sin(x)+\frac{1}{2}sin(2x)+\frac{1}{3}sin(3x)+....))
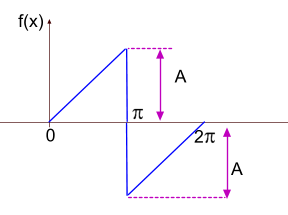
=\frac{2A}{\pi}(sin(x)-\frac{1}{2}sin(2x)+\frac{1}{3}sin(3x)-....))
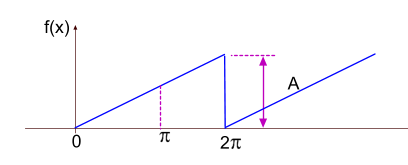
=\frac{A}{2}-\frac{A}{\pi}(sin(x)+\frac{1}{2}sin(2x)+\frac{1}{3}sin(3x)+....))
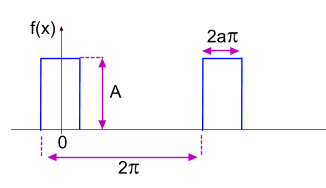
=A(\alpha+\frac{2}{\pi}(sin(\aplha\pi)cos(x)+\frac{1}{2}sin(2\aplha\pi)cos(2x)+\frac{1}{3}sin(3\aplha\pi)cos(3x)+..+\frac{1}{n}sin(n\alpha\pi)cos(nx))))