| Координаты многоугольника, разделенные пробелами в формате x+iy | |
В данной статье мы окажем помощь в расчете периметра многоугольника, заданного координатами его вершин. Несмотря на то, что сам принцип расчета прост, при большом количестве вершин, Вам придется делать несколько раз одни и те же вычисления, то есть выполнять рутинную операцию. А я страсть как не люблю рутину и Вам ей заниматься не советую.
Формула которая используется проста:
Если извеcтны две точки с координатами (x1,y1) и (x2,y2) то расстояние между ними
эту формулу необходиом применить к каждой паре координат соседних вершин многоугольника. И как только мы закончим обход и просуммировав все длины мы получим наш периметр.
Теперь что касается ввода данных. В предыдущем материале Площадь многоугольника по координатам онлайн ввод координат осуществляется через двоеточие и пробел, что не совсем удобно.
В этой статье, для упрощения и для обощения ( на комплексное представление) коодинаты будут задаватся в виде комплексных чисел.
Для тех кто с комплексными числами никогда не сталкивался, хочу успокоить - ничего страшного.
И если Вы координату раньше представляли как (x,y), то в комплексном представлении эта же координата видится уже как x+iy
Для ввода это немного проще, так как в дальнейшем при написании статьи про линейные преобразования фигуры на плоскости, это форма ввода нам пригодится, да и понимать ту статью Вам будет уже намного проще.
Теперь немного примеров:
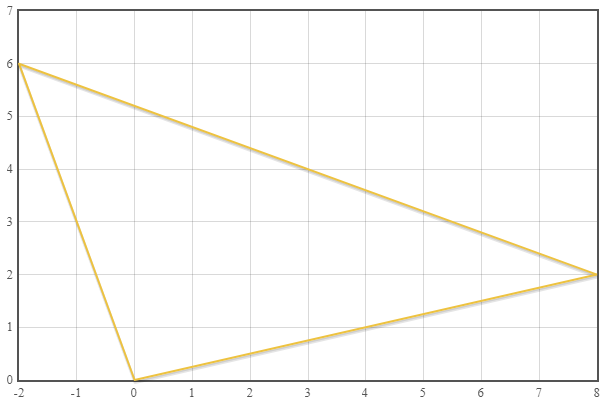
Определим периметр многоугольника заданного координатами А (0; 0); В (8; 2); С (–2; 6).
Так как три вершины то это треугольник.
Введем данные в поле ввода( разделяя каждую координату вершины пробелом) в таком формате 0+0i 8+2i -2+6i
Получаем результат
| Вы ввели следующие координаты многоугольника |
 |
| Периметр многоугольника (в условных единицах) |
|
25.341096185841
|














^2+(y2-y1)^2})