| Радиус первой окружности |
| Радиус второй окружности |
| Расстояние между двумя окружностями |
| Площадь пересечения двух окружностей равна: |
Позволяет рассчитать площадь пересечения двух окружностей произвольных радиусов.
Используются достаточно простые формулы, которые элементарно доказываются.
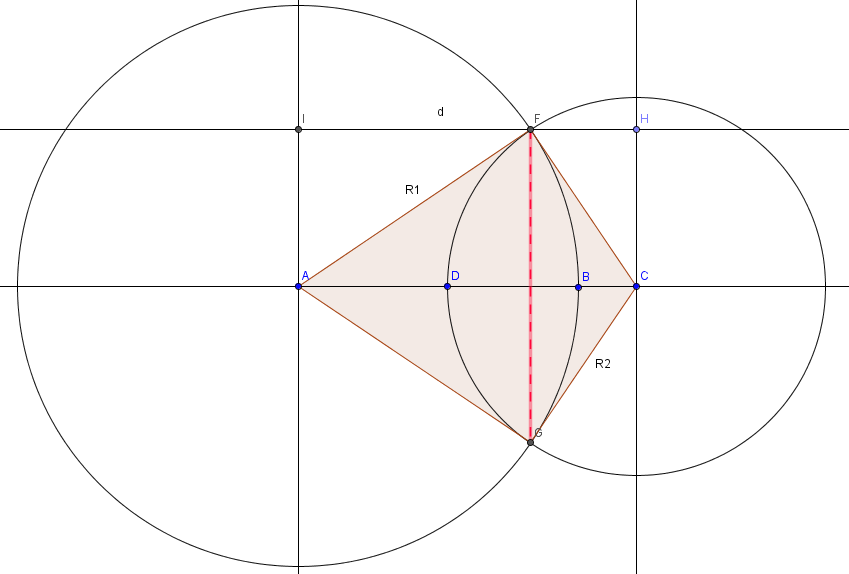
Площадь пересечения двух окружностей состоит из двух сегментов FDG и FBG
Вывести формулу расчета площади пересечения двух окружностей можно из двух общеизвестных формул и знаний решения треугольника:
Формулы сектора окружности
и длина хорды окружности
По известным сторонам треугольника AFС определяем высоту на сторону AC.
Удвоением этой высоты мы получаем длину хорды, после этого узнаем угол альфа по второй формуле.
По известным сторонам треугольника AFG узнаем его площадь. Вычитаем её из площади сектора окружности, ведь угол альфа нам уже известен.
И получаем площадь сегмента FBG
Подобным образом вычисляем FDG
Это лишь один из способов решения задачи вычисления площади пересечения двух окружностей.
где
{tex}F_1=2*acos{{R_1^2-R_2^2+D^2} \over 2*R_1*D}{/tex}
{tex}F_2=2*acos{{R_2^2-R_1^2+D^2} \over 2*R_2*D}{/tex}
где
{tex}R_1{/tex} - радиус первой окружности
{tex}R_2{/tex} - радиус второй окружности
{tex}D{/tex} - расстояние между центрами окружностей
Пример
Хотим узнать площадь пересечения двух окружностей радиусом в 1 и расстоянием между центрами 0.8079455
Пишем okr 1 1 0.8079455
Ответ
Площадь двух пересекающихся окружностей равна = 1.5707963388681~ PI/2
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 3
Пишем okr 4 2 3
Ответ
Площадь двух пересекающихся окружностей равна = 9.5701994729833
Первая окружность радиус 4, вторая окружность радиус 2, расстоянием между центрами 0
Пишем okr 4 2 0
Ответ
Окружности не пересекаются















)

) \over 2})
) \over 2})