Расчет расстояния от прямой до точки

Параметры прямой и координаты точки

Уравнение прямой в различных видах

Общее уравнение прямой

Уравнение прямой с угловым коэффициентом

Уравнение прямой в отрезках

Нормальное уравнение прямой

Расстояние между заданной точкой и прямой составляет(в условных единицах)

Расчет расстояния от прямой до точки

В школьной программе есть задачи на нахождение кратчайшего расстояния точки до прямой.

Прямая может быть задана или формулой или двумя координатами.

уравнение прямой

если прямая линия задана формулой {tex}Ax+By+C=0{/tex} то расчет растояния до точки (x1,y1)осуществляется по следующим формулам

{tex}\delta=\frac{Ax1+By1+C}{\pm\sqrt{A^2+B^2}}{/tex}

Так как расстояние не может быть отрицательным, то знак + или - означает лишь следующее:

Значение {tex}\delta{/tex} положительно, если точка и начало координат лежат по разные стороны от прямой, и отрицательно, если по одну сторону.

В принице, Вы можете воспользоваться универсальным определителем параметров прямой Расчет параметров прямой линии по заданным параметрам

Характеристики прямой могут быть достаточно разнообразны:

Прямую можно задать с помощью двух координат (xa:ya) и (xb:yb)

Можно задать в виде коэффициентов A, B и C прямой выраженной в виде $Уравнение прямой$

или в виде значений k и a прямой выраженной в виде $уравнение прямой с угловым коэффициентом$

а также в любых других видах, в параметрическом или прямой в отрезках.

Точка с координатами (x0:y0) - это как раз та точка рассстояние между которой и прямой и надо определить.

Примеры

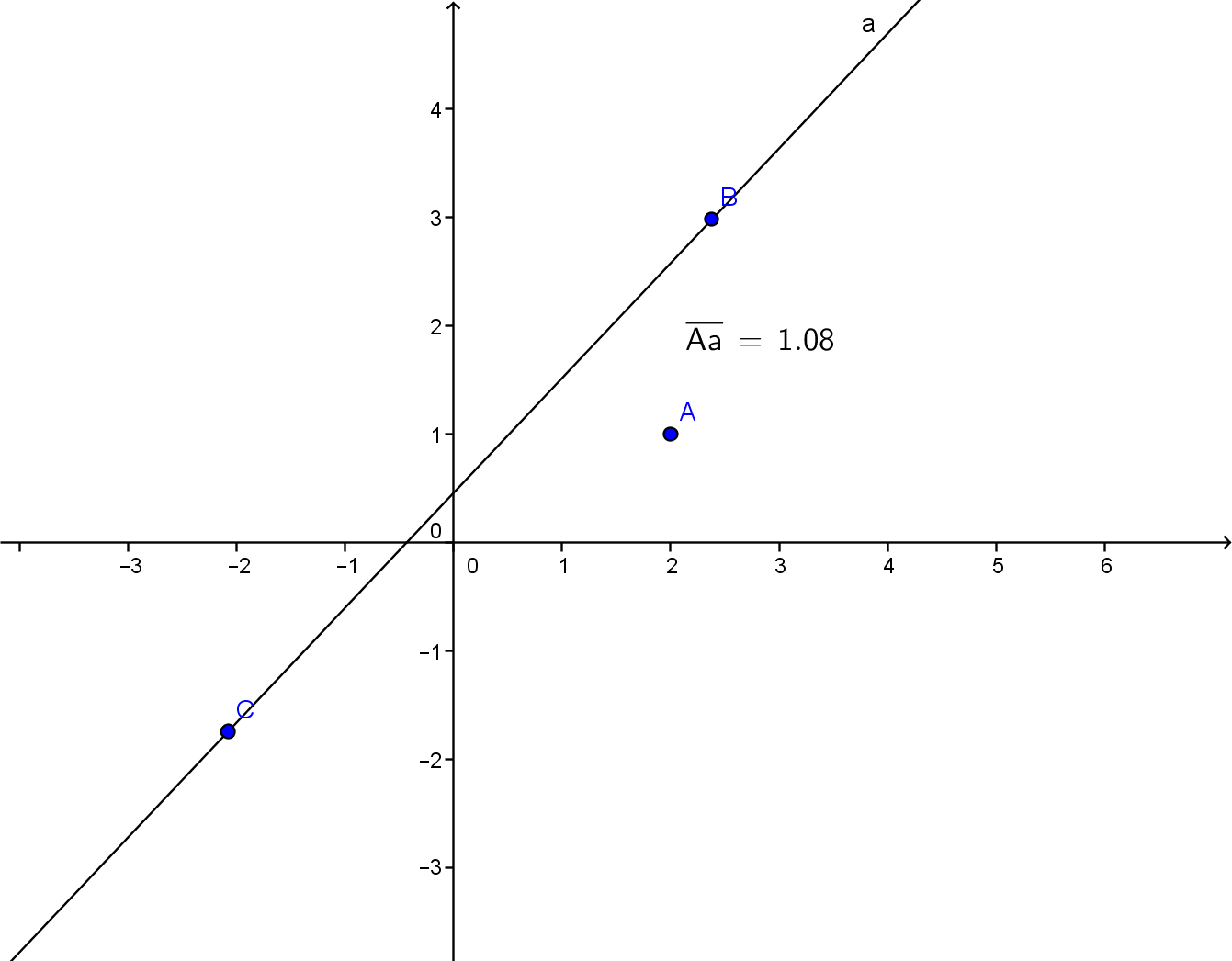
Найти расстояние между точкой с координатами (2:1) и прямой, проходящей через две точки: (2.38:2.98) и (-2.08:-1.74)

Логично предположить что нам известно

xa, xb, ya yb - это параметры прямой линии

а x0 и y0 - это координаты точки

так и запишем в запросе

line xa=2.38;ya=2.98;xb=-2.08;yb=-1.74;x0=2;y0=1

В ответе получаем

Параметры прямой линии по заданным параметрам

Общее уравнение Ax+By+C=0

Коэффициент А=4.72

Коэффициент B=-4.46

Коэффициент C=2.0572

Уравнение прямой в отрезках x/a+y/b = 1

Коэффициент a=-0.43584745762712

Коэффициент b=0.46125560538117

Уравнение прямой c угловым коэфициентом y = kx + b

Коэффициент k=1.0582959641255

Угол наклона к оси ( в градусах) f=46.622322587496

Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0

Коэффициент p=-0.31679237157357

Коэффициент q=2.3845093608736

Расстояние между точками=6.4938432380217

Расстояние от точки до прямой dp = -1.0836726021959

Таким образом наш ответ 1.0836726021959

Знак минус говорит о том, что начало координат и точка лежат по одну сторону от заданной прямой

Найти расстояние до точки (-4:-2) до прямой, заданная уравнением 3x+4y=5

Пишем следующий запрос

line x0=-4;y0=-2;A=3;B=4;C=-5

Получаем ответ

Параметры прямой линии по заданным параметрам

Общее уравнение Ax+By+C=0

Коэффициент А=3

Коэффициент B=4

Коэффициент C=-5

Уравнение прямой в отрезках x/a+y/b = 1

Коэффициент a=1.6666666666666

Коэффициент b=1.25

Уравнение прямой c угловым коэфициентом y = kx + b

Коэффициент k=-0.75

Угол наклона к оси ( в градусах) f=-36.869897645844

Нормальное уравнение прямой x*cos(q)+y*sin(q)-p = 0

Коэффициент p=-0.99999999999998

Коэффициент q=0.92729521800162

Расстояние между точками=

Расстояние от точки до прямой dp = -4.9999999999999

Ответ на задачу = 4.9999999 то есть 5

и как можно убедиться на рисунке, точка начала кординат и заданная точка лежит тоже на одной стороне от заданной прямой