| Населенный пункт |
| Местное время в виде ДД/ММ/ГГГГ/ЧЧ/ММ/СС |
| Заданное время в населенном пункте |
| Географическая широта долгота |
| Время по Гринвичу |
| Звездное время |
| Юлианская дата |
| Временный пояс |
Звездное время
Время обращения Земли вокруг оси можно измерить, наблюдая суточное вращение небесной сферы.
Продолжительность полного оборота небесной сферы можно определить с большой степенью точности как промежуток времени между двумя последовательными одноименными (например, верхними) кульминациями какой-либо звезды или определенной точки небесной сферы. В качестве такой точки выбирают точку весеннего равноденствия (Т).
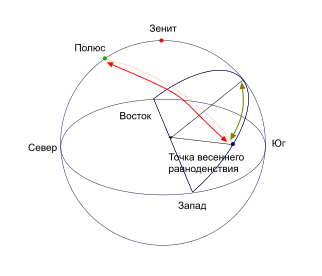
Промежуток времени между двумя последовательными верхними кульминациями точки весеннего равноденствия называется звездными сутками.
За начало звездных суток принимается момент верхней кульминации точки Т.
Звездные сутки делятся на 24 звездных часа, час — на 60 минут, минута — на 60 секунд. Легко видеть, что положение точки Т относительно меридиана, характеризуемое дугой небесного экватора, заключенной между меридианом и точкойТ и отсчитываемой в направлении суточного вращения небесной сферы (помечена зеленовайто стрелкой), определяет долю суток, протекшую с начала данных суток до рассматриваемого момента. Иначе говоря, указанная дуга экватора является мерой времени в данный момент. Так как эта дуга в градусной мере равна сферическому углу, образованному меридианом и большим кругом, проведенным через полюс и точку Т (отображена красной стрелкой) и называемую часовым углом, то мы приходим к следующему определению: звездное время S в данный момент равно часовому углу точки весеннего равноденствия. Так как сутки разделены на 24 часа, а окружность содержит 360°, то получат следующие соотношения:
1 чаc = 15°, 1 минута — 15', 1 секунда — 15".
Поскольку час, минута и секунда представляют единицы измерения часового угла, то и обозначения этих единиц ставятся, подобно обозначениям единиц градусной меры, вверху справа соответствующей цифры. Следовательно, запись момента времени будет выглядеть так: S = 14ч06м27с.
Звездное время используется при астрономических наблюдениях. В житейских целях оно неудобно, так как наша жизнь согласуется с Солнцем.
Солнечное время
По аналогии со звездными сутками вводится понятие истинных солнечных суток, которыми называется промежуток времени между двумя последовательными верхними кульминациями центра солнечного диска.
Истинным солнечным временем называется часовой угол (/0) центра Солнца. Так как Солнце в результате годичного движения по эклиптике перемещается в сторону, обратную суточному движению, приблизительно на 1° в сутки, то истинные солнечные сутки длиннее звездных в среднем приблизительно на 4 мин.
Неравномерность течения истинного солнечного времени
Истинное солнечное время неудобно в том отношении, что очень трудно построить часы, идущие по этому времени, так как часовой угол Солнца меняется неравномерно. Это происходит, во-первых, в результате неравномерности движения Солнца по эклиптике и, во-вторых, вследствие наклона эклиптики к экватору. Перемещения Солнца по эклиптике вблизи перигелия и афелия за равные промежутки времени будут неодинаковыми, а равным перемещениям Солнца по эклиптике вблизи точек равноденствия.и солнцестояния будут соответствовать неодинаковые изменения часового угла (рис. 38).
Среднее эклиптическое и среднее экваториальное Солнце
Для устранения неравномерности истинного солнечного времени вводят понятие «среднего Солнца», подразумевая под этим термином некоторую вспомогательную движущуюся точку. «Средним эклиптическим солнцем» называется точка, равномерно движущаяся по эклиптике и проходящая через перигелий и афелий одновременно с центром истинного солнечного диска. Замена истинного Солнца «средним эклиптическим» устраняет неравномерность солнечного времени, вызываемую непостоянством скорости движения Солнца по эклиптике. Для устранения влияния наклона эклиптики к экватору вводится понятие «среднего экваториального солнца», представляющего собой точку, равномерно движущуюся по экватору и проходящую через точки весеннего и осеннего равноденствия одновременно со «средним эклиптическим солнцем».
Среднее солнечное время
Воображаемое «среднее экваториальное солнце» участвует в суточном вращении небесной сферы так же, как и истинное Солнце. Промежуток времени между двумя последовательными одинаковыми кульминациями «среднего экваториального солнца» называется средними сутками. За начало средних суток принимают момент пижкей кульминации «среднего экваториального солнца». Часовой угол «среднего экваториального солнца» определяет среднее время в данный момент. Средние сутки делятся на 24 средних часа, час—на 60 мин и минута — на 60 сек.
Поясное время
Каждый пункт на поверхности Земли имеет свое собственное местное время, которое отличается (в зависимости от долготы) от времени другого пункта на любое число часов, минут и секунд. В практической жизни пользоваться местным временем очень неудобно, особенно для транспорта и связи. Это обстоятельство поставило задачу упорядочения счета времени на всей Земле. В настоящее время эта задача разрешена введением системы поясного времени.
Весь земной шар по меридианам через каждые 15° разбит на 24 пояса. Середина "начального или нулевого" пояса проходит через Гринвичский меридиан и во всем этом поясе принято местное время Гринвичского меридиана. В следующем восточном поясе принято местное время среднего меридиана этого пояса, отличающееся от мирового времени на час и т. д. Это время обозначается Та и называется поясным, а пояса называются часовыми.
В любом пункте Земли поясное время отличается от местного примерно на полчаса (максимально). Введение поясного времени приводит к тому, что в ряде населенных пунктов, находящихся в непосредственной близости друг от друга, время отличается на час. Однако это искупается тем, что минуты и секунды на всем земном шаре при пользовании поясным временем одинаковы и время различных пунктов отличается друг от друга только на целое число часов.
Границы часовых поясов проводят, в ряде случаев отступая от меридианов, по государственным, административным или естественным (рекам, горным хребтам) границам
Линия изменения даты
Местное или поясное время, считая к востоку от нулевого меридиана (проходящего через Гринвич), будет возрастать пропорционально долготе. Если рассматривать местное время, считая к западу от нулевого меридиана» то местное время будет убывать. В связи с этим рассмотрим следующий факт.
Пусть три наблюдателя, находясь на одном и том же месте средней широты, начинают одновременно счет дням, отмечая их по восходу Солнца, причем первый остается на месте, второй отправляется в кругосветное путешествие по параллели на восток, а третий — в кругосветное путешествие по параллели на запад. Когда все три наблюдателя снова соберутся в одном месте, то оставшимся на месте наблюдатель скажет, что между встречами прошло N суток, а путешествовавший в восточном направлении скажет, что прошло (N + 1) суток. Это обусловлено тем, что второй наблюдатель при движении к востоку будет наблюдать кульминацию Солнца каждый раз несколько раньше, чем неподвижный наблюдатель.
Наблюдатель, путешествовавший в западном направлении, скажет, что прошло (N - 1) суток, так как, двигаясь в сторону, обратную вращению Земли, он будет наблюдать кульминацию Солнца каждый раз с некоторым запозданием по сравнению с неподвижным наблюдателем.
Чтобы согласовать счет дней, для неподвижных наблюдателей и путешественников по международному соглашению введена «линия перемены даты». Она вся расположена по прверхности океана и проходит приблизительно по 180 меридиану, считая от Гринвича. При пересечении этой линии в западном направлении из счета дней выбрасывается один день (например, за вторым числом при записях сразу следует четвертое число). При пересечении линии перемены даты в восточном направлении при счете дней приписывается лишний день (например, при записях какое-либо число повторяется дважды).
Счет меридианов от Гринвича удобен, ибо при этом линия перемены даты приходится на удобную для запоминания цифру (180°) долготы, что не будет иметь места, если счет меридианам вести от какой-либо другой обсерватории.













